


Выпишем эллипсоид вращения - поверхность, которая получается в результате вращения эллипса
\[
\frac{x^2}{a^2}+\frac{z^2}{c^2}=1
\]
вокруг оси $z$. Соответствующее уравнение, в соответствии с (40), получается заменой $x \rightarrow \sqrt{x^2+y^2}$:
\begin{equation}
\frac{x^2+y^2}{a^2}+\frac{z^2}{c^2}=1. (41)
\label{ellipsd1}
\end{equation}
В зависимости от соотношения величин $a,\,c$ мы получаем несколько разный вид поверхности. При $a>c$ поверхность называется сжатый эллипсоид вращения, при $a Рис 17: Сжатый эллипсоид вращения. Рис 18: Вытянутый эллипсоид вращения. Если растянуть координату $y$, то мы получим уравнение общего эллипсоида
\begin{equation}
\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1. (42)
\label{ellipsd11}
\end{equation}
Если ввести сечение поверхности плоскостью, параллельной оси $z$ (т.е. зафиксировать значение $z=z_0$ в уравнении), то для эллипсоидов вращения мы получим окружность (при $|z_0| Задачи. Выпишем уравнение гиперболы в координатах $(x,z)$ в виде
\[
\frac{z^2}{c^2}-\frac{x^2}{a^2}=1,
\]
и рассмотрим результат вращения этой кривой вокруг оси $z$. В этом случае получим уравнение однополостного гиперболоида вращения:
\[
\frac{z^2}{c^2}-\frac{x^2+y^2}{a^2}=1,
\]
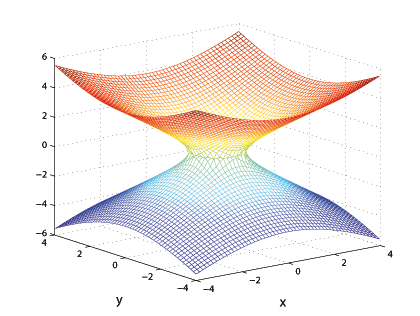
Рис 19: Однополостный гиперболоид вращения. см. рис. 19. Эта неограниченная поверхность, связная (т.е. такая, что из фиксированной точки можно достичь любой другой, не покидая поверхность). Ее сечения плоскостями $x=const, \, y=const$ представляют собой гиперболы, а сечения плоскостью $z=const$ являются окружностями.
Иная поверхность получится, если мы рассмотрим результат вращения гиперболы
\[
\frac{x^2}{a^2}-\frac{z^2}{c^2}=1,
\]
вокруг оси $z$, соответствующая поверхность называется двуполостным гиперболоидом вращения. Выпишем ее уравнение:
\[
\frac{x^2+y^2}{a^2}-\frac{z^2}{c^2}=1.
\]
Это также неограниченная поверхность, однако она состоит "из двух кусков", см. рис. 19
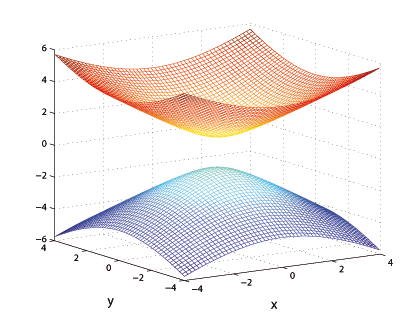
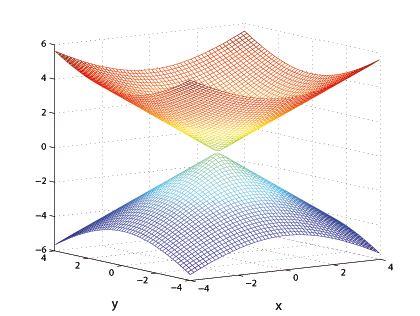
Рис 20: Двуполостный гиперболоид вращения. Ее сечения плоскостями $x=const, \, y=const$ представляют собой гиперболы, а сечения плоскостью $z=const$ ( при тех значения $const$, при которых сечения существуют) являются окружностями.
Предельным случаем гиперболоида является круговой конус - результат вращения вокруг оси $z$ пары прямых
\[
\frac{x^2}{a^2}=\frac{z^2}{c^2},
\]
см. рис. \ref{konus}. Уравнение этой поверхности получается в результате стандартной процедуры,
\[
\frac{x^2+y^2}{a^2}=\frac{z^2}{c^2}.
\]
Рис 21: Круговой конус. Сечения этой поверхности плоскостями $x=const \neq 0, \, y=const \neq 0$, - гиперболы, сечения плоскостями $z=const \neq 0$ - окружности. Сечения плоскостями $x=0$, $y=0$ - пары пересекающихся прямых, плоскостью $z=0$ - точка.
Разумеется, с помощью растяжений координат можно поверхности вращения превратить в более общие, которые мы здесь обсуждать не будем. Задачи. Если мы рассмотрим результат вращения параболы $x^2=2pz$ вокруг оси $z$, то получим параболоид вращения
\[
x^2+y^2=2pz,
\]
см. рис. 22.
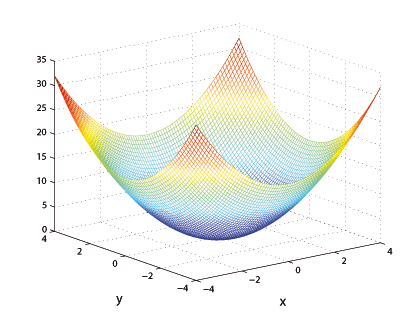
рис. 22: Параболоид вращения. Растягивая оси $x$ и $y$, получим эллиптический параболоид
\[
\frac{x^2}{a^2}+\frac{y^2}{b^2}=2z.
\]
Сечения этой поверхности плоскостями $x=const, \, y=const$ представляют собой параболы, сечения плоскостями $z=const>0$ - эллипсы.
Если в последнем уравнении поменять знак у второго слагаемого, получим гиперболический параболоид
\[
\frac{x^2}{a^2}+\frac{y^2}{b^2}=2z,
\]
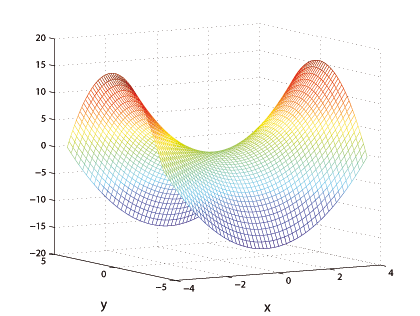
см. рис. 23. рис. 23: Гиперболический параболоид. Эту поверхность используют для описания т.н. "седловых" точек. Ее сечения плоскостями $x=const, \, y=const$ - параболы, сечения плоскостями $z=const \neq 0$ - гиперболы, плоскостью $z=0$ - пара пересекающихся прямых. Задачи.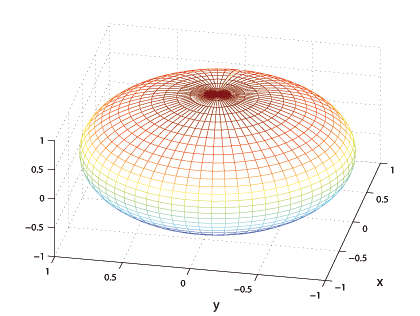
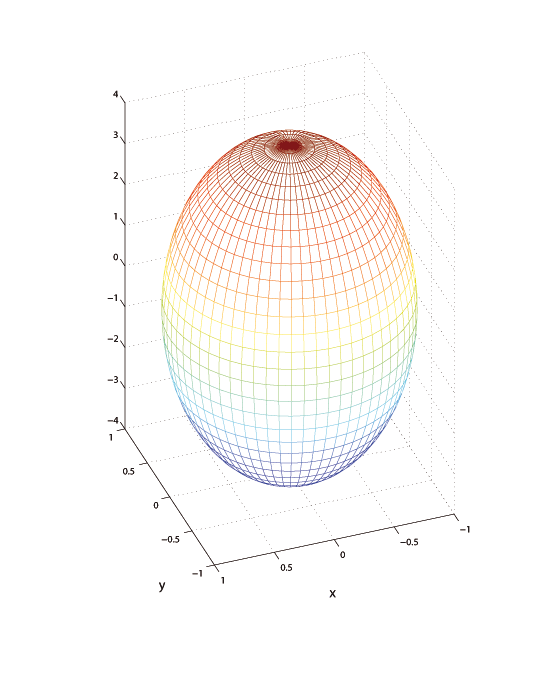
5.2.2 Гиперболоиды
5.2.3 Параболоиды