4. Аналитическая геометрия в трехмерном пространстве

4.3 Плоскость в трехмерном пространстве

Для фиксации плоскости в трехмерном пространстве фиксируем сначала точку $M_0$, через которую проходит плоскость. Однако через точку можно провести много плоскостей. Для однозначной фиксации плоскости следует задать вектор ее нормали $\textbf {N}$, которой ортогональна плоскость вместе со всеми прямыми на ней, см. рис. 14.

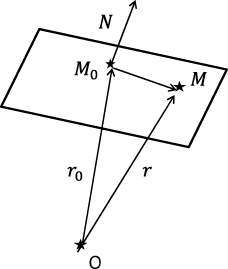
Рис 14: Плоскость в трехмерном пространстве задается фиксированной точкой $M_0$ и фиксированной нормалью $N$.

Рассмотрим вектора $\textbf {r}_0=OM_0$ и $\textbf {r}=OM$. Вектор $\textbf {r-r}_0$ лежит на плоскости и ортогонален нормали $N$, \[ (\textbf {r-r}_0, \textbf {N})=0. \] Раскрывая скобки скалярного произведения, получаем: \begin{equation} (\textbf {r}, \textbf {N})=d, \quad d=(\textbf {r}_0, \textbf {N}). \label{pl1} \end{equation} Это уравнение называется векторным уравнением плоскости. Пусть $\textbf {r}=x\textbf {i}+y\textbf {j}+z\textbf {k}$, $\textbf {N}=A\textbf {i}+B\textbf {j}+C\textbf {k}$, тогда это уравнение перепишется в виде \begin{equation} Ax+By+Cz+D=0, \quad D =-d. (31) \label{pl2} \end{equation} Это уравнение называется общим уравнением плоскости. Отметим, что по виду этого уравнения можно построить вектор нормали $\textbf {N}=(A,B,C)^T$. Если $ D\neq 0$, то уравнение (31) можно, перенося $D$ направо и деля все уравнение на $-D$, переписать в виде \begin{equation} \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1, (32) \label{pl22} \end{equation} это уравнение называется уравнением плоскости в отрезках. Геометрический смысл параметров $a,\,b,\,c$ - величина отрезков, отсекаемых плоскостью на осях координат. Есть еще один способ задания плоскости в трехмерном пространстве. Если вектора $\textbf {p}=(p_1,\,p_2,\,p_3)^T, \,\textbf {q}=(q_1,\,q_2,\,q_3)^T$ лежат на плоскости, и если они линейно независимы, то любой вектор можно представить как их линейную комбинацию. Так, вектор $\textbf {r}-\textbf {r}_0$ можно представить в виде \[ \textbf {r}-\textbf {r}_0=t_1\textbf {p}+t_2\textbf {q}. \] Выписывая это соотношение по координатам, имеем: \begin{equation} x-x_0=t_1p_1+t_2q_1, \quad y-y_0=t_1p_2+t_2q_2, \quad z-z_0=t_1p_3+t_2q_3, (33) \label{pl5} \end{equation} это параметрические уравнения плоскости. Когда параметры $t_1, \, t_2$ пробегают значения в пределах $(-\infty, \, \infty)$, точка $M$, соответсвующая вектору $\textbf {r}$, пробегает всю плоскость. Если заданы три точки $M_0=(x_0,\, y_0, \, z_0)$ , $M_1=(x_1,\, y_1, \, z_1)$, $M_2=(x_2,\, y_2, \, z_2)$, не лежащие на одной прямой, через них можно провести плоскость. Выпишем уравнение этой плоскости. Покажем, что его можно записать в вид: \begin{equation} \left| \begin{array}{ccc} x-x_0 &y-y_0 & z-z_0 \\ x_1-x_0&y_1-y_0 &z_1-z_0 \\ x_2-x_0 &y_2-y_0 &z_2-z_0 \end{array} \right| =0. (34) \label{pl6} \end{equation} В самом деле, если написать разложение этого определителя по первой строке, мы получим уравнение вида (31), т.е. уравнение плоскости. Осталось проверить, что исходные точки удовлетворяют этому уравнению. Подставляя, например, вместо $x, \, y, \,z$ значения $x_0, \, y_0, \,z_0$, получим нулевую строку определителя, так что он равен нулю, т.е. точка $M_0$ удовлетворяет уравнению (34). Аналогично проверяется и для двух других точек. Угол между плоскостями можно определить, вычисляя угол между нормалями к плоскостям, \[ \cos \varphi = \frac{(\textbf {N}_1,\, \textbf {N}_2)}{|\textbf {N}_1|\cdot |\textbf {N}_2|}. \] Далее, расстояние от заданной точки $(x_0,\,y_0,\,z_0)$ до плоскости (31) вычисляется согласно формуле \begin{equation} L=\frac{Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}}. (35) \label{dist} \end{equation}

Пример.

Контрольный вопрос.

Решение типовых задач.

Задачи.