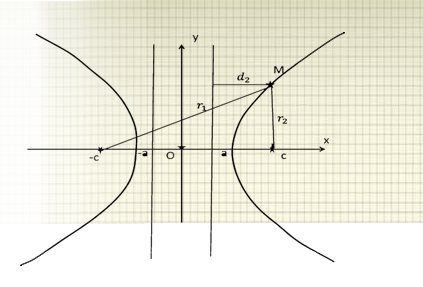
3. Аналитическая геометрия на плоскости
3.7 Парабола
Выпишем каноническое уравнение параболы, записанное в канонической системе координат,
\begin{equation}
y^2=2px, \quad p>0, (25)
\label{par1}
\end{equation}
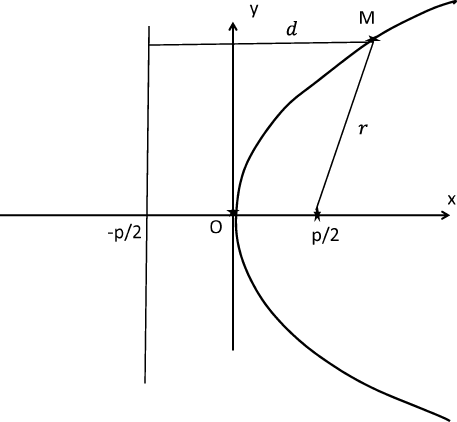
Рис 7: Парабола и ее директриса.
Из уравнения следует, что для всех точек $x \geq 0$. Далее, переменная $y$ входит в это уравнение во второй степени, так что если точка $(x,y)$ лежит на параболе, то и точка $(x,-y)$ лежит на параболе. Т.о., парабола симметрична при отражении относительно оси $x$.
Точка $(p/2, \, 0)$ называется фокусом параболы. Директрисой параболы называется прямая $x=-p/2$.
Теорема. Для того, чтобы точка лежала на параболе, необходимо и достаточно, чтобы ее расстояния до фокуса и директрисы совпадали.
Доказательство.
1. Достаточность. Расстояние до директрисы для точки $(x,y)$ равно $x+p/2$, фокальный радиус равен
\[
\sqrt{(x-p/2)^2+y^2}.
\]
Приравнивая и возводя в квадрат, получаем:
\[
x^2+px+\frac{p^2}{4}=x^2-px+\frac{p^2}{4}+y^2.
\]
Приводя подобные члены, приходим к (25).
2. Необходимость. Имеем:
\[
r=\sqrt{(x-p/2)^2+y^2}=\sqrt{x^2-px+p^2/4+y^2},
\]
подставляя $y^2=2px$, получаем под корнем полный квадрат от $d^2=x+p/2$. ч.т.д.
Решение типовых задач.
Задача 1.
Определить координаты фокуса и составить уравнение директрисы для параболы $3y^2 + 12y - 18x + 12 = 0$.
Решение.
С помощью несложных преобразований приведем заданное уравнение параболы к каноническому виду:
\[
3(y^2 + 4y + 4) - 18x = 0,
\]
\[
3(y + 2)^2 = 18x,
\]
\[
(y + 2)^2 = 2\cdot 3x.
\]
Из последнего уравнения следует, что вершина параболы расположена в точке $\textbf{A}(0,-2)$, а параметр $p=3$. Следовательно, фокусом является точка $\textbf{F}\left( \frac{3}{2},-2 \right)$, а директрисой является прямая $x=-\frac{3}{2}$.
Задача 2.
Составить уравнение параболы, если известно, что ее фокус находится в точке пересечения прямой $4x-3y-4=0$ с осью абсцисс.
Решение.
Несложно заметить, что точкой пересечения прямой $4x-3y-4=0$ с осью абсцисс является точка $\textbf{F}(1,0)$.
По условию эта точка является фокусом параболы, следовательно, параметр $p=2$. Тогда уравнение параболы записывается как $y^2 = 4x$.
Задача 3.
Найти уравнение прямой, проходящей через центр окружности $x^2 + y^2 + 8x -4y -3 = 0$ параллельно прямой, соединяющей фокус параболы $y = 4 x^2$ и правый фокус эллипса $\frac{x^2}{13}+\frac{(y-1)^2}{9}=1$.
Решение.
Приведем уравнение окружности к каноническому виду
\[
(x + 4)^2 + (y-2)^2 -16 -4 -3 = 0,
\]
\[
(x + 4)^2 + (y-2)^2 = 23.
\]
Таким образом, центром окружности является точка $\textbf{O}(-4,2)$.
Далее, фокусом параболы $y = 4 x^2$ является точка $\textbf{A}(1,0)$.
Правый фокус эллипса $\frac{x^2}{13}+\frac{(y-1)^2}{9}=1$ находится в точке с координатами $\textbf{B}(\sqrt{a^2+b^2},1)$, т.е. в точке $\textbf{B}(2,1)$.
Запишем уравнение прямой, проходящей через точки $\textbf{A}(1,0)$ и $\textbf{B}(2,1)$:
\[
\frac{x-1}{2-1}=\frac{y-0}{1-0}.
\]
В результате получим прямую $y-x+1=0$.
Искомая прямая есть прямая, параллельная $y-x+1=0$ и проходящая через точку $\textbf{O}(-4,2)$, т.е. имеющая вид $y-x+C=0$. Константу $C$ найдем, подставив координаты точки $\textbf{O}$: $2-(-4)+C=0$, т.е. $C=-6$.
Таким образом, уравнение искомой прямой есть $y-x-6=0$.
Задачи.
1. Определить координаты фокуса и составить уравнение директрисы для параболы $y^2=6x$.
2. Определить точки пересечения прямой $x+y-3=0$ и параболы $x^2=4y$.
3. На параболе $y^2=16x$ найти точки, фокальный радиус которых равен 13.
4. Через точку $М(2, 1)$ проведена хорда параболы $y^2=4x$ , которая делится в этой точке пополам. Найти ее уравнение.
5. Вычислить длину сторон правильного треугольника, вписанного в параболу $y^2=2px$.
6. Найти точки пересечения параболы $y^2=12x$ с эллипсом
\[
\frac{x^2}{25}+\frac{y^2}{16}=1.
\]
7. Через фокус параболы $y^2=2px$ проведена хорда, перпендикулярная оси параболы. Вычислить ее длину.
8. На параболе $y^2=8x$ найти точку, фокальный радиус которой равен 20.
9. Составить уравнения сторон треугольника, вписанного в параболу $y^2=8x$ так, что отдна из его вершин совпадает с вершиной параболы, а точка пересечения высот совпадает с фокусом параболы.
10. Через точку $(2,1)$ провести хорду параболы $y^2=4x$, делящуюся в этой точке пополам.