3. Аналитическая геометрия на плоскости
3.6 Гипербола
Каноническое уравнение гиперболы
\begin{equation}
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1, (22)
\label{hyp1}
\end{equation}
соответствующий рисунок 6.
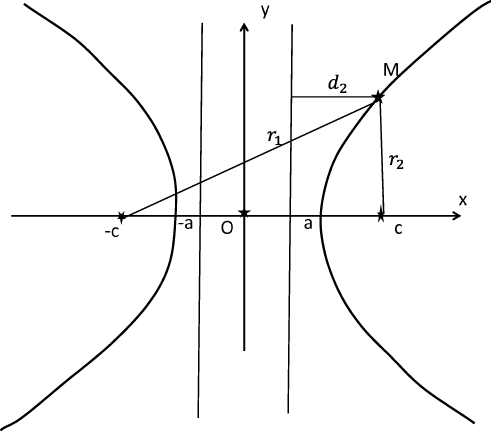
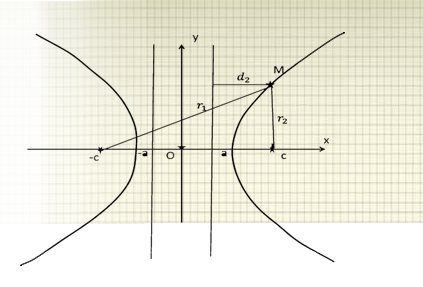
Рис 6: Гипербола и ее директрисы.
Это уравнение, напомним, выполняется в специальной системе координат, которая называется канонической. Числа $a, \, b$ называются вещественной и мнимой полуосями гиперболы. Точки $(\pm a, \, 0)$ называются вершинами гиперболы.
Выпишем элементарные свойства гиперболы.
1. Из уравнения следует, что $|x| \geq a$.
2. Так как переменные $x,y$ входят в уравнение гиперболы только в квадратах, то из того, что $(x,y)$ лежат на гиперболе следует, что точки $(\pm x, \, \pm y)$ также лежат на гиперболе при любом выборе знаков. Это означает, что гипербола симметрична при отражении относительной осей координат и имеет центр симметрии, точку $O$.
3. Гипербола состоит из двух ветвей, содержит точки, сколь угодно далекие от начала координат.
4. Решая уравнение (22) относительно переменной $y$, получаем:
\[
y=\pm b \sqrt{\frac{x^2}{a^2}-1}.
\]
Когда $|x| \rightarrow \infty$, ветви гиперболы приближаются к прямым $y=\pm bx/a$. Эти прямые называются асимптотами гиперболы, она лежит между ними.
Положим для гиперболы $c=\sqrt{a^2+b^2}$, эксцентриситет $\varepsilon = c/a$. Эксцентриситет описывает вытянутость гиперболы. Точки $(\pm c, \, 0)$ называются фокусами гиперболы. Как следует из определений, $c>a$, так что для гиперболы $\varepsilon >1$. Отрезки, соединяющие точку $M$ гиперболы с ее фокусами, называются фокальными радиусами точки $M$.
Уравнение гиперболы очень похоже на уравнение эллипса, отличие - в знаке одного из членов уравнения. Поэтому и описание гиперболы в определенном смысле параллельно описанию эллипса. Доказательство теорем по существу повторяет доказательство аналогичных результатов для эллипса.
Теорема. Для того, чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы модуль разности ее фокальных радиусов равнялась $2a$,
\begin{equation}
|r_1-r_2|=2a. (23)
\label{hyper2}
\end{equation}
Доказательство.
1. Достаточность. Из рисунка получаем:
\[
r_1=\sqrt{(x+c)^2+y^2}, \quad r_2=\sqrt{(x-c)^2+y^2},
\]
так что выполняется условие (для определенности рассматриваем правую ветвь гиперболы, так что $r_1>r_2$)
\[
\sqrt{(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2}=2a.
\]
Покажем, что отсюда следует, что $(x,y)$ удовлетворяет уравнению (22). Надо избавиться от корней. Для этого перенесем один из корней направо и возведем в квадрат. Раскрывая скобки, получаем:
\[
x^2+2xc+c^2+y^2=4a^2+4a\sqrt{(x-c)^2+y^2}+x^2-2xc+c^2+y^2.
\]
Сокращая подобные члены и деля на 4, получаем:
\[
a\sqrt{(x-c)^2+y^2}=xc -a^2.
\]
Возводя еще раз в квадрат, приходим к формуле:
\[
a^2(x^2-2xc+c^2+y^2)=a^4-2a^2xc+x^2c^2.
\]
Сокращая еще раз подобные члены, получаем:
\[
(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2).
\]
Подставляя $c^2=a^2+b^2$, получаем соотношение, только множителем отличающееся от соотношения (22).
2. Необходимость. Пусть выполняется (22), вычислим $r_1$. Имеем:
\[
r_1=\sqrt{(x+c)^2+y^2}=\sqrt{(x+c)^2+b^2-\frac{b^2x^2}{a^2}}=\sqrt{x^2+2xc+c^2+\frac{b^2x^2}{a^2}-b^2}=
\]
\[
\sqrt{\frac{c^2x^2}{a^2}+2xc+a^2}=a+\varepsilon x.
\]
Вычисление $r_2$ по этой схеме приводит к результату (имеется отличие только в одном знаке!) $r_2=\varepsilon x -a$, из свойств гиперболы следует, что в правой части - положительное число. Вычитая, получаем (23). ч.т.д.
Имеется еще одно описание эллипса. Введем т.н. директрисы гиперболы - прямые $x=\pm a/\varepsilon$, см. рис. 6. В данном случае $\varepsilon >1$, так что директрисы лежат между вершинами гиперболы.
Теорема. Для того, чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы отношение расстояния от этой точки до фокуса к расстоянию до соответствующей директрисы было равно эксцентриситету гиперболы,
\begin{equation}
r_2/d_2=\varepsilon. (24)
\label{hyp3}
\end{equation}
Доказательство.
1. Достаточность. Пусть $r_2=\varepsilon d_2$. Из рисунка следует, что $d_2=a/ \varepsilon -x$, так что
\[
\sqrt{(x-c)^2+y^2}=a-\varepsilon x.
\]
Возводя в квадрат, получаем:
\[
x^2+2xc+c^2+y^2=a^2+2\varepsilon x+\varepsilon ^2x^2.
\]
Приводя подобные члены и учитывая явное выражение для $\varepsilon $, получаем:
\[
\frac{b^2x^2}{a^2}+y^2=b^2.
\]
Это соотношение, после домножения на подходящий множитель, переходит в (22).
2. Необходимость. Пусть точка $(x,y)$ лежит на гиперболе, т.е. выполняется уравнение (22). Как было показано при доказательстве предыдущей теоремы, мы получаем $r_2=\varepsilon x -a$. Из рисунка: $d_2=x-a / \varepsilon $. Делим одно на другое - получаем (24). ч.т.д.
\textit{\textbf {Пример}}. Пусть известно следующее: фокусное расстояние $c=10$, она проходит через точку $(12, \, 3\sqrt{5})$. Напишем уравнение этой гиперболы. Подставляя точку в каноническое уравнение гиперболы, получаем:
\[
\frac{144}{a^2}-\frac{45}{b^2}=1,
\]
Обозначая $b^2=s$, получим квадратное уравнение $s^2+89s-4500=0$. Его положительное решение $s=36$. Соответственно, $a^2=100-36=64$. Таким образом, искомая гипербола имеет вид
\[
\frac{x^2}{64}-\frac{y^2}{36}=1,
\]
Решение типовых задач.
Задача 1.
Написать уравнение гиперболы и уравнения ее асимптот, если вещественная полуось равна $\sqrt{15}$ и гипербола проходит через точку $\textbf{M} (5,\sqrt{6})$.
Решение.
По условию $a=\sqrt{15}$. Длину мнимой полуоси найдем, подставив в каноническое уравнение гиперболы координаты точки $\textbf{M}$:
\[
\frac{5^2}{15}-\frac{6}{b^2}=1
\]
Отсюда $b=3$. Тогда можно записать каноническое уравнение гиперболы
\[
\frac{x^2}{15}-\frac{y^2}{9}=1
\]
и уравнения асимптот $y=\pm \frac{3}{\sqrt{15}}x$.
Задача 2.
Написать уравнение гиперболы с фокусами $F_1(-7;0)$ и $F_2(7;0)$, проходящей через
точку $\textbf{M}(-2;12)$.
Решение.
Найдем фокальные радиусы точки $\textbf{M}$:
\[
r_1 = |MF_1| = \sqrt{(-7-(-2))^2+(0-12)^2}=13, \,
\]
\[
r_2 = |MF_2| = \sqrt{(7-(-2))^2+(0-12)^2}=15.
\]
Согласно приведенной выше теореме, модуль разности фокальных радиусов равен длине большой оси гиперболы: $|r_1-r_2|=2a$, следовательно, в нашем случае имеем $|13-15|=2a$. Значит длина большой полуоси $a=1$.
По условию $c=7$. Тогда из соотношения $c=\sqrt{a^2+b^2}$ выразим малую полуось - $b=\sqrt{c^2-a^2}=\sqrt{49-1}=\sqrt{48}$.
Запишем каноническое уравнение гиперболы
\[
x^2 - \frac{y^2}{48}=1.
\]
Задача 3.
Написать каноническое уравнение гиперболы, если ее эксцентриситет равен 2 и фокусы совпадают с фокусами эллипса $\frac{x^2}{25}+\frac{y^2}{16}=1$.
Решение.
Найдем координаты фокусов эллипса, для них выполняется соотношение $c^2=a^2-b^2$. Т.е., в нашем случае $c^2=25-16=9$. Тогда, точки $F_1(-3;0)$ и $F_2(3;0)$ являются фокусами и эллипса и гиперболы.
Эксцентриситет вычисляется по формуле $\varepsilon=\frac{c}{a}$, следовательно, $a=\frac{c}{\varepsilon} = \frac{3}{2}$.
Кроме того, для гиперболы справедливо соотношение $c^2=a^2+b^2$. Тогда $b^2=c^2-a^2=9-\frac{9}{4}=\frac{27}{4}$.
Таким образом, искомое уравнение гиперболы имеет вид $\frac{4x^2}{9}-\frac{4y^2}{27}=1$.
Задачи.
1. Написать уравнение гиперболы, полуось которой равна половине фокусного расстояния эллипса
\[
\frac{x^2}{169}+\frac{y^2}{144}=1,
\]
а фокусное расстояние гиперболы равно большой оси эллипса.
2. Написать каноническое уравнение гиперболы, если угол между ее асимптотами равен 60 градусов, и гипербола проходит через точку $(4\sqrt{3},2)$.
3. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом
\[
\frac{x^2}{49}+\frac{y^2}{24}=1,
\]
эксцентриситет которой равен 1,25.
4. Составить уравнение гиперболы, имеющей общие фокусы с эллипсом
\[
\frac{x^2}{35}+\frac{y^2}{19}=1,
\]
и проходящей через точку $(4\sqrt{2},3)$.
5. Написать уравнение гиперболы, проходящей через точки $(6,-1)$, $(-8, 2\sqrt{2})$.
6. Вычислить фокальные радиусы для точки (-5;9/4), лежащей на гиперболе
\[
\frac{x^2}{16}-\frac{y^2}{9}=1.
\]
7. Определить угол между асимптотами гиперболы, у которой эксцентриситет равен 2.
8. Вычислить полуоси гиперболы, асимптоты которой даны уравнениями $y = \pm 2x$ и фокусы находятся на расстоянии 5 от центра.
9. На гиперболе
\[
\frac{x^2}{16}-\frac{y^2}{9}=1
\]
найти точку, для которой расстояние от левого фокуса в 2 раза больше, чем расстояние от правого фокуса.
10. Через точку $(3,-1)$ провести хорду гиперболы
\[
\frac{x^2}{4}-y^2=1,
\]
делящуюся в этой точке пополам.