3. Аналитическая геометрия на плоскости

3.8 Кривые второго порядка в полярных координатах

Для кривых второго порядка - эллипса, гиперболы и параболы - можно получить простое описание в полярных координатах. Для этого надо поместить начало координат в фокусе (мы выбираем правый фокус) и полярную ось совместить с положительным направлением оси $x$.

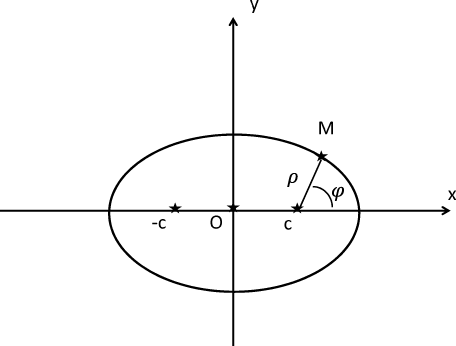
Рис 8: Эллипс в полярной системе координат.

1. Эллипс.

Описанная система координат изображена на рис. 8. При обсуждении эллипса была получена формула для фокального радиуса: $\rho = a-\varepsilon x$. Из рисунка следует: $x=c+\rho \cos \varphi$. Подставляя, получаем: \[ \rho = a-\varepsilon c-\varepsilon \rho \cos \varphi. \] Собирая слагаемые с $\rho $, приходим к уравнению \[ \rho=\frac{p}{1+\varepsilon \cos \varphi}, \quad p=a-\varepsilon c. \] Это и есть уравнение эллипса в полярной системе координат. Отметим следующие обстоятельства. В знаменателе стоит выражение, положительное при всех значениях $\varphi $ - потому что для эллипса $\varepsilon <1$. Поэтому из этого уравнения следует, что эллипс имеет точки при всех углах $\varphi $, причем при всех углах значения $\rho$ конечны.

2. Гипербола.

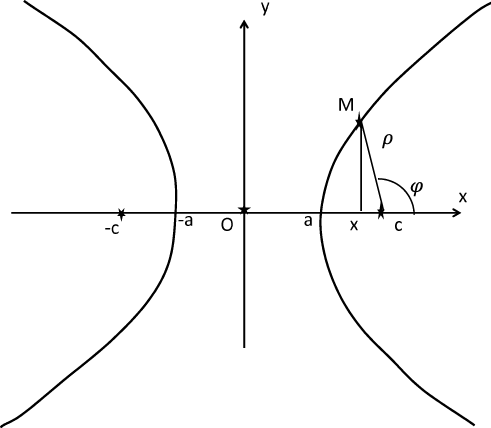
Рис 9: Гипербола в полярной системе координат.

Для гиперболы имеем, согласно проведенным выше вычислениям, $\rho = \varepsilon x-a$. Из картинки 9 следует, что $x=c+\rho \cos \varphi$. Подставляя это значение и собирая слагаемые с $\rho $, получаем: \[ \rho =\frac{p}{1+\varepsilon \cos \varphi}, \quad p=a-\varepsilon c, \] уравнение гиперболы в полярной системе координат. Формально это уравнение совпадает с уравнением эллипса, однако имеется важное отличие: $\varepsilon >1$. Это означает, что есть углы, для которых знаменатель отрицателен - при этих значениях угла гипербола не имеет точек. Для двух значений угла знаменатель обращается в 0, так что при этих углах $\rho$ обращается в бесконечность. Т.о., гипербола неограниченная кривая. Это уравнение описывает одну ветвь (правую) гиперболы.

3. Парабола.

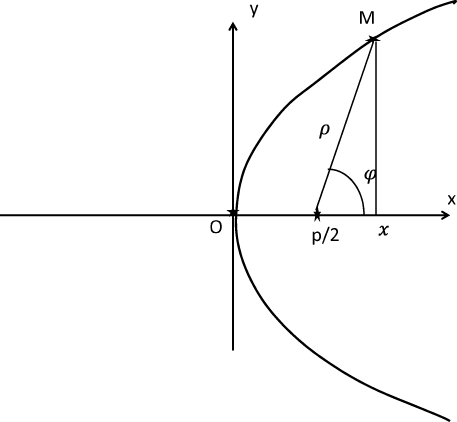
Рис 10: Парабола в полярной системе координат.

Пусть точка $M=(x,y)$ лежит на параболе. Согласно приведенным выше вычислениям, $\rho = x+p/2$, а согласно картинке 10 имеем: $x=p/2 +\rho \cos \varphi $. Подставляя в первое соотношение и собирая слагаемые с $\rho$, получаем: \[ \rho =\frac{p}{1-\cos \varphi}. \] Это и есть уравнение параболы в полярной системе координат. Отметим, что только при $\varphi = 0 $ знаменатель обращается в ноль, что соответствует обращению в $\infty$ величины $\rho$. Таким образом, парабола также содержит бесконечно удаленные точки. Отметим, что уравнения всех трех кривых в полярной системе координат по существу совпадают - отличается только один коэффициент в знаменателе, точнее, допустимые значения этого параметра. Для эллипса он от нуля до единицы, для гиперболы - больше единицы, а для параболы равен -1. Эти значения и определяют различия этих кривых.