3. Аналитическая геометрия на плоскости

3.9 Касательные

Пусть на плоскости задана кривая уравнением $F(x,y)=0$ (т.е. неявным образом). Пусть точка $(x_0, y_0)$ принадлежит этой кривой. Выпишем уравнение касательной к кривой в этой точке. Напомним, что если кривая задана уравнением $y=f(x)$, то, как известно из курса дифференциального исчисления, угловой коэффициент касательной в точке $(x_0,y_0)$, лежащей на кривой, равен значению производной $f(x)$ в этой точке, т.е. $k=f'(x_0)$. Таким образом, уравнение касательной (уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку) имеет вид: \[ y-y_0=f'(x_0)(x-x_0). \] Если кривая задана неявно, то производная $f'(x_0)$ вычисляется согласно соотношению \[ f'(x_0)=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}|_{x_0, y_0}. \] Подставляя в уравнение касательной, получаем уравнение касательной в окончательном виде: \begin{equation} (y-y_0)\cdot \frac{\partial F}{\partial y}(x_0, y_0)+(x-x_0)\cdot \frac{\partial F}{\partial x}(x_0, y_0)=0. (26) \label{kasat} \end{equation} Рассмотрим с помощью этого соотношения касательные к кривым второго порядка.

1. Касательная к эллипсу. Исходное уравнение \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, \] так что $\frac{\partial F}{\partial x}=\frac{2x}{a^2}$, $\frac{\partial F}{\partial y}=\frac{2y}{b^2}$. При этом уравнение (26) принимает вид \[ \frac{2(x-x_0)x_0}{a^2}+\frac{2(y-y_0)y_0}{b^2}=0. \] Сокращая на 2 и учитывая, что точка $(x_0,y_0)$ лежит на эллипсе, получаем уравнение касательной эллипса, проходящей через эту точку: \begin{equation} \frac{xx_0}{a^2}+\frac{yy_0}{b^2}=1. (27) \label{kasell} \end{equation}

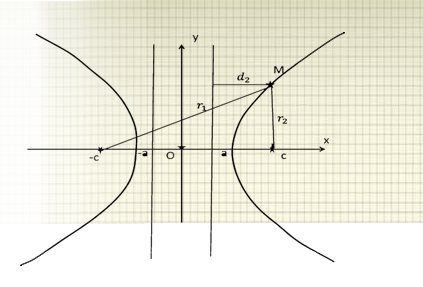
2. Касательная к гиперболе. Исходное уравнение \[ \frac{x^2}{a^2}-\frac{y^2}{b^2}=1, \] так что $\frac{\partial F}{\partial x}=\frac{2x}{a^2}$, $\frac{\partial F}{\partial y}=-\frac{2y}{b^2}$. При этом уравнение (26) принимает вид \[ \frac{2(x-x_0)x_0}{a^2}-\frac{2(y-y_0)y_0}{b^2}=0. \] Сокращая на 2 и учитывая, что точка $(x_0,y_0)$ лежит на гиперболе, получаем уравнение касательной гиперболы, проходящей через эту точку: \begin{equation} \frac{xx_0}{a^2}-\frac{yy_0}{b^2}=1. (28) \label{kashyp} \end{equation}

3. Касательная к параболе. Исходное уравнение \[ y^2-2px=0, \] так что $\frac{\partial F}{\partial x}=-2p$, $\frac{\partial F}{\partial y}=2y$. При этом уравнение (26) принимает вид \[ -2p(x-x_0)+2(y-y_0)y_0=0. \] Сокращая на 2 и учитывая, что точка $(x_0,y_0)$ лежит на параболе, получаем уравнение касательной параболы, проходящей через эту точку: \begin{equation} yy_0=p(x+x_0). (29) \label{kaspar} \end{equation}

Пример.

Задачи.