1. Введение
2. Основные структуры
- 2.1 Элементы теории множеств
- 2.2 Операции с множествами
- 2.3 Функции и способы их задания
- 2.4 Числовые последовательности
3. Пределы. Непрерывные функции
- 3.1 Предел последовательности
- 3.1.1 Определения
- 3.1.2 Арифметика пределов
- 3.1.3 Арифметика бесконечно малых
- 3.1.4 Признаки существования пределов
- 3.1.5 Вычисление пределов
- 3.1.6 Замечательный предел
- 3.2 Функции непрерывной переменной
- 3.2.1 Определения
- 3.2.2 Арифметика пределов
- 3.2.3 Арифметика бесконечно малых
- 3.2.4 Признаки существования пределов
- 3.2.5 Замечательные пределы
- 3.2.6 Список важнейших предельных соотношений
- 3.3 Непрерывные функции
- 3.3.1 Определения
- 3.3.2 Основные свойства
- 3.3.3 Разрывы функции
4. Производная, дифференциальное исчисление
- 4.1 Производная
- 4.1.1 Определение производной
- 4.1.2 Производная от элементарных функций
- 4.1.3 Производная от суммы, произведения и частного функций
- 4.1.4 Производные от сложной функции, от обратной функции, от функции, заданной параметрически
- 4.1.5 Таблица производных
- 4.2 Первый дифференциал
- 4.2.1 Определение и основные свойства первого дифференциала
- 4.2.2 Геометрический смысл первого дифференциала
- 4.2.3 Дифференциал сложной функции. Инвариантность первого дифференциала
- 4.3 Свойства дифференцируемых функций
- 4.4 Правило Лопиталя и раскрытие неопреленностей
5. Высшие производные
- 5.1 Определение и свойства высших производных
- 5.2 Определение и свойства дифференциалов высших порядков
- 5.3 Теорема Тейлора
- 5.4 Формула Тейлора для некоторых функций
6. Приложения дифференциального исчисления
- 6.1 Монотонность функции и знак ее производной
- 6.2 Достаточное условие локального максимума/минимума
- 6.3 Решение задачи о глобальном максимуме/минимуме функции на замкнутом отрезке
- 6.4 Выпуклость вверх, выпуклость вниз, точки перегиба
7. Первообразная (неопределенный интеграл)
- 7.1 Определение и основные свойства первообразных
- 7.2 Таблица основных первообразных
- 7.3 Интегрирование по частям
- 7.4 Замена переменной в первообразной
8. Техника вычисления первообразных
- 8.1 Интегралы от дробно-рациональных функций
- 8.1.1 Полиномы, основные свойства
- 8.1.2 Дробно-рациональные функции, основные свойства
- 8.1.3 Выделение целой части и разложение на простейшие для дробно-рациональных функций
- 8.1.4 Вычисление первообразной от дробно-рациональной функции
- 8.2 Интегралы от тригонометрических функций
- 8.3 Интегралы от функций, содержащих иррациональности
- 8.4 Подстановки Эйлера
- 8.5 "Неберущиеся" интегралы
9. Определенный интеграл
- 9.1 Определение
- 9.2 Геометрический смысл определенного интеграла
- 9.3 Основные свойства
- 9.4 Формула Ньютона-Лейбница
- 9.4.1 Интеграл как функция верхнего предела
- 9.4.2 Формула Барроу
- 9.4.3 Формула Ньютона-Лейбница
- 9.5 Интегрирование по частям в определенном интеграле
- 9.6 Замена переменной в определенном интеграле
10. Несобственные интегралы
- 10.1 Несобственные интегралы 1 рода
- 10.1.1 Определение и основные свойства
- 10.1.2 Признаки сходимости несобственных интегралов 1 рода
- 10.2 Несобственные интегралы 2 рода
- 10.2.1 Определение и основные свойства
- 10.2.2 Признаки сходимости несобственных интегралов 2 рода
11. Интегралы зависящие от параметра
12. Приложения определенных интегралов
4. Производная, дифференциальное исчисление
4.2 Первый дифференциал
4.2.1 Определение и основные свойства первого дифференциала
Пусть в некоторой окрестности точки $x_0$ задана функция $y=f(x)$, причем $f(x)$ дифференцируема в точке $x_0$.
Определение. Первым дифференциалом функции $f(x)$ в точке $x=x_0$ называется выражение $df(x_0,\Delta x)=f'(x_0)\cdot \Delta x$, где величина $\Delta x$ предполагается достаточно малой.
Замечание. Если $f(x)=x$, то имеем: $dx=\Delta x$. Это равенство выполняется, когда $x$ является независимой переменной.
Из определения производной следует, что \[ \frac{\Delta f}{\Delta x}=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \xrightarrow[\Delta x\to 0]{} f'(x_0), \] так что \[ \frac{\Delta f}{\Delta x} - f'(x_0) = \alpha (\Delta x), \quad \alpha (\Delta x)\xrightarrow[\Delta x\to 0]{} 0. \] Умножая на $\Delta x$, получаем: \[ \Delta f=df(x_0, \Delta x)+\alpha (\Delta x)\cdot \Delta x, \quad \alpha (\Delta x)\xrightarrow[\Delta x\to 0]{} 0. \]
Следовательно, при малых $\Delta x$ имеем приближенное равенство: \[ \Delta f \approx df. \]
Это приближенное равенство (и его аналоги) играют ключевую роль в приближенных вычислениях.
Описанные выше свойства производной приводят к соответствующим свойствам первого дифференциала. Если заданы две дифференцируемые функции $u(x)$, $v(x)$, то
1. $d(c \cdot u)=c \cdot du$.
2. $d(u+c)=du$.
3. $d(u+v)=du+dv$.
4. $d(u\cdot v)=du \cdot v+u \cdot dv.$
5. $d(u/v)=(du\cdot v-u\cdot dv)/v^2.$
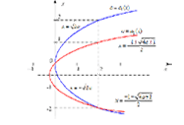
4.2.2 Геометрический смысл первого дифференциала
Рассмотрим график функции $y=f(x)$ в окрестности точки $x$ и касательную к графику, проведенную через точку $(x,f(x)$.

Рис 3: К геометрическому смыслу первого дифференциала
Из картинки ясно, что отрезок $df$ - это то, что отсекают касательная и прямая $y=f(x)$ на вертикальной прямой, проходящей через $x+\Delta x$.
4.2.3 Дифференциал сложной функции. Инвариантность первого дифференциала
Пусть $y=f(x)$, $z=h(y)$, причем эти функции дифференцируемы при всех интересующих нас $x,y$. Подставляя $y=f(x)$ в аргумент функции $z=h(y)$, получим сложную функцию $z=h(f(x))$. Выпишем ее первый дифференциал, \[ dz=\left(h(f(x))\right)'\Delta x. \] Используя правило дифференцирования сложной функции, получаем: \[ dz=\frac{dh}{dy}\cdot \frac{df}{dx}\Delta x. \] Однако согласно определению первого дифференциала, $\frac{df}{dx}\Delta x =dy$, так что предыдущее равенство переписывается в виде: \[ dz=\frac{dh}{dy}dy. \]
Это равенство выглядит точно также, как если бы мы полагали нашу функцию зависящей от независимой переменной $y$, забыв о том, что мы имеем дело со сложной функцией. Этот факт и называется инвариантностью первого дифференциала.
Задачи.