Функции и способы их задания
Задачи.
1. В круговой конус высоты $H$ с радиусом основания $R$ вписан цилиндр (образующая цилиндра при этом полагается параллельной оси конуса). Определить площадь боковой поверхности и объем цилиндра как функции радиуса цилиндра $r$. Найти области определения этих функций.
2. Пусть функция $f(x)$ имеет областью определения интервал $(0,1)$. Найти области определения функций $f(x^2)$, $f(\sin x)$, $f(\ln x)$.
3. Показать, что суперпозиция двух дробно-линейных функций \[ f(x)=\frac{a_1x+b_1}{a_2x+b_2}, \quad x=\phi (t)=\frac{c_t+d_1}{c_2t+d_2} \] является дробно-линейной функцией и найти выражение для ее коэффициентов.
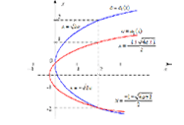
4. Найти обратные функции и построить их графики для функций
a) $$f(x)=\frac{8+x^3}{8-x^3}$$
б) $$f(x)=\sqrt{x-4}$$
Предел последовательности. Замечательный предел
Задачи.
Вычислить пределы $a_n$ при $n \rightarrow +\infty$.
1. \[ a_n=\frac{(2n^3-3n+1)^{1/3}}{2n-7}. \]
2. \[ a_n=\frac{(20n^2+3)^{1/3}}{2n+5}. \]
3. \[ a_n=\frac{(n+1)^3-(n-1)^3}{n^2+7n+1}. \]
4. \[ a_n=\frac{(n+2)!-n!}{(n+1)!}. \]
5. \[ a_n=\frac{(n^5+1)^{1/3}-(n^2+5)^{1/2}}{(n^4+3)^{1/2}-2}. \]
6. \[ a_n=\frac{1+2+3+...+n}{n+1}-\frac{n+1}{2} \]
Функции непрерывной переменной. Список важнейших предельных соотношений
Задачи.
Вычислить пределы.
1. \[ \lim _{x \rightarrow 0 } \frac{ 3x^3-2x+1}{10x^4-2x^3+2}. \]
2. \[ \lim _{x \rightarrow 1 } \frac{x^3-1}{x^4+3x^2-1}. \]
3. \[ \lim _{x \rightarrow -1 } \frac{x^2+4x-1}{x^3+1}. \]
4. \[ \lim _{x \rightarrow 0 } \frac{(1-2x)^{1/4}-(1+3x)^{1/3}}{\sin 2x}. \]
5. \[ \lim _{x \rightarrow 0 } \frac{\sqrt{x^2+4}-2}{\sqrt{x^2+16}-4}. \]
6. \[ \lim _{x \rightarrow 2 } \frac{\sqrt{x-2}-\sqrt{2}+\sqrt{x}}{\sqrt{x^2-4}}. \]
7. \[ \lim _{x \rightarrow +0 } \frac{ 1-\cos 2x}{5 x^2} . \]
8. \[ \lim _{x \rightarrow 0 } \frac{4x^2-3x}{2x^2-9x}. \]
9. \[ \lim _{x \rightarrow +\infty} \frac{ x^5-2x^3+11x}{3x^5+2x^3-3} . \]
10. \[ \lim _{x \rightarrow +0} (\cos x)^{2/x^2} . \]
Непрерывные функции. Разрывы функции
Задачи.
Найти и исследовать точки разрыва функций:
1. $$y=e^{\frac{1}{x-2}}.$$
2. $$y=\frac{1}{x^2-4}.$$
3. $$y=\sin \left(\frac{\pi }{x+3}\right).$$
4. $$y=arctg \left(\frac{1}{x}\right ). $$
Производная. Производный от суммы, произведения и частного функций
Задачи.
Вычислить значение производной в указанной точке.
1. Вычислить $f'(4)$, $$f(x)=3x^2-2\sqrt{x}.$$
2. Вычислить $f'(1)$, $$f(x)=\frac{x^3-5x+1}{x^2}.$$
3. Вычислить $f'(2)$, $$f(x)=\frac{3}{5-x}+x^2/3.$$
Вычислить производную от указанных функций.
1. $ y(x)=3x^3+4x+7.$
2. $ y(x)=x^4-x^3/3+2x-1$.
3. $y(x)=(x^3-2x-1)(x^3+x^2+1).$
4. $ y(x)=\sqrt{x}(x^3+2\sqrt{x}-1).$
5. $y(x)=(x+1)^2(x-1).$
6. $y(x)=x\cdot e^x.$
7. $y(x)=x^2\cdot \sin x.$
8. $y(x)=e^x\cdot(\sin x+\cos x).$
9. $$y(x)=\frac{1}{1+x^2}.$$
10. $$y(x)=\frac{x^2+x+1}{x^3+1}.$$
11. $$y(x)=\frac{1-x^3}{1-x^5}.$$
12. $$y(x)=tg x+\frac{e^x}{1+x}.$$
13. $$y(x)=\frac{\sqrt{x}+3x^3-1}{7+2x}.$$
14. $$ y(x)=\frac{\sin x}{1+\cos x}.$$
15. $$y(x)=\frac{\arcsin x}{\arccos x}$$.
Производная. Производные от сложной функции, от обратной функции, от функции, заданной параметрически
Задачи. Вычислить производную от указанных функций.
1. $y(x)=\sin (\sqrt{x})$.
2. $y(x)=\sqrt{\cos x}$.
3. $y(x)=\sqrt{1+2x-x^2}$.
4. $y(x)=\sin (2x)+2\cos (3x)$.
5. $$y(x)=\frac{x}{\sqrt{1-x^2}}$$.
6. $y(x)=\sqrt{1+\ln x}$.
7. $y(x)=(\arcsin x)^3.$
8. $y(x)=\ln (\sin x+1).$
9. $y(x)=a^x$.
10. $y(x)=arctg x^2.$
11. $y(x)=\ln (x^2-4x).$
12. $$y(x)=\arcsin \left(\frac{2}{x}\right).$$
13. $$y(x)=\frac{x^4}{4^x}.$$
14. $y(x)=e^{\arcsin 2x}.$
15. $y(x)=\sin (x/2)\sin 2x.$
16. $y(x)=\sin (e^{\cos x}).$
Первый дифференциал. Дифференциал сложной функции. Инвариантность первого дифференциала
Задачи.
1. Найти дифференциалы функций
а) $y=3x^3+6x-4$.
б) $y=\sin x-x\cos 2x$.
в) $y=\cos(\ln x))$.
2. Вычислить приближенно значения функций, используя первый дифференциал.
а) $f(x)=x^5-2x^3-5x^2+7$ при $x=1.001$.
б) $f(x)=x\ln(x-2)$ при $x=3.003$.
в) $f(x)=\sqrt{4x^3-2x^2-1}$ при $x=1.002$.
Правило Лопиталя и раскрытие неопреленностей
Задачи. Вычислить пределы.
1. \[ \lim _{x \to a}\frac{e^x-e^a}{x-a}. \]
2. \[ \lim _{x \to 0}\frac{e^x-e^{-x}}{\ln (1+x)}. \]
3. \[ \lim _{x \to 0}\frac{e^x-e^{-x}-2x}{x-\sin x}. \]
4. \[ \lim _{x \to 2}\frac{\ln(x^2-3)}{x^2+3x-10}. \]
5. \[ \lim _{x \to 0}\left(\frac{1}{x^2}-ctg ^2x\right ). \]
Определение и свойства высших производных
Задачи.
1. $f(x)=e^{-x^2}$. Вычислить $f''(x)$.
2. $f(x)=x^{3/5}$. Вычислить $f'''(x)$.
3. $f(x)=x\sin^2x$. Вычислить $f'''(x)$.
4. $f(x)=x\ln x$. Вычислить $f^{(4)}(x)$.
5. $f(x)=e^x\cos x$. Вычислить $f'''(x)$.
Теорема Тейлора
Задачи.
1. Применив формулу Тейлора с остаточным членом в форме Лагранжа к функции $f(x)=e^x$, вычислить с абсолютной погрешностью не больше $0.001$ значение $e^{0.11}$.
2. Разложить многочлен $f(x)=x^4-4x^3-2x-3$ по степеням двучлена $x-2$.
3. Написать формулу Тейлора 3-го порядка для функции $f(x)=\arcsin 2x$ при $x_0=0$.
4. Написать формулу Тейлора 4-го порядка для функции $f(x)=xe^x$ при $x_0=0$.
Монотонность функции и знак ее производной
Задачи. Найти интервалы монотонности функции
1. $f(x)=x^3-3x^2-9x+2$.
2. $f(x)=x-e^x$.
3. $f(x)=x^2-2\ln x$.
Достаточное условие локального максимума /минимума
Задачи. Найти экстремальные точки функции и выяснить их характер.
1. $f(x)=x^2-6x+8.$
2. $f(x)=x^2(x-4).$
3. $f(x)=\sin x-x.$
4. $f(x)=\sin x-x+x^3/3.$
Решение задачи о глобальном максимуме/минимуме функции на замкнутом отрезке
Задачи.
1. Найти наибольшее и наименьшее значение функции $f(x)=x^3-6x$ на интервале $\left[ -3,4\right]$.
2. Найти стороны прямоугольника наибольшего периметри, вписанного в полуокружность радиуса $R$.
3. Окно имеет форму прямоугольника, завершенного сверху полукругом. Какими должны быть размеры, если фиксирован периметр окна, а площадь должна быть наибольшей?
4. Кусок проволоки имеет фиксированную длину. Ее разрезают на 2 части, затем из одной делают квадрат, из второй - окружность. Как надо разрезать проволоку, чтобы сумма площадей круга и квадрата была наибольшей?
Выпуклость вверх, выпуклость вниз, точки перегиба
Задачи.
1. Показать, что функция $f(x)=x^2+x^4$ везде выпукла вниз.
2. При каких значениях $a,b$ точка $A(3,1)$ является точкой перегиба кривой $f(x)=ax^2+bx^3$?
Таблица основных первообразных
Вычислить первообразные.
1. \[ \int (3x^3-2x^4+7)dx\,. \] 2. \[ \int \sqrt{x}dx. \] 3. \[ \int a^xb^xdx. \] 4. \[ \int \cos(3x-4)dx. \] 5. \[ \int \frac{5-3\sqrt[3]{x^2}+2\sqrt[5]{x}}{\sqrt[3]{x}}dx. \] 6. \[ \int \frac{1-x^2}{x^2(1+x^2)}dx. \] 7. \[ \int \sin(2x+7)dx. \] 8. \[ \int \frac{(1-x)^3}{x\sqrt{x}}dx. \] 9. \[ \int \left(\frac{1-x}{x}\right)^2dx. \] 10. \[ \int (\sqrt{x}+1)(x+1)dx. \] 11. \[ \int \frac{dx}{x^2}. \] 12. \[ \int \cos^2(2x+3)dx. \] 13. \[ \int \frac{dx}{1-\cos2x}. \] 14. \[ \int \frac{\sin ^4xdx}{\cos ^2x}. \]
Интегрирование по частям
Вычислить первообразные.
1. \[ \int xlnxdx. \]
2. \[ \int x\sin xdx. \]
3. \[ \int xe^{-x}dx. \]
4. \[ \int xarctg xdx. \]
5. \[ \int x\cos (2x) dx. \]
6. \[ \int x\cos^2xdx. \]
7. \[ \int x4^xdx. \]
8. \[ \int x^2a^xdx. \]
Замена переменной в первообразной
Вычислить первообразные
1. \[ \int \frac{\sqrt{lnx}}{x}dx. \] 2. \[ \int \frac{x}{\sqrt[3]{x^2+1}}dx. \] 3. \[ \int \frac{dx}{(arcsinx)^3\sqrt{1-x^2}}. \] 4. \[ \int \frac{x^3}{\sqrt{1-x^8}}dx. \] 5. \[ \int \frac{dx}{\cos ^2x(3tgx+1)}. \] 6. \[ \int \frac{\cos (3x)dx}{4+\sin(3x)}. \] 7. \[ \int \frac{dx}{1+\sqrt{x+1}}. \] 8. \[ \int \frac{x^2dx}{\sqrt{x-1}}. \] 9. \[ \int \frac{dx}{x\sqrt{x-1}}. \] 10. \[ \int \frac{\sqrt{x}dx}{x+1}. \]
Вычислить первообразные от дробно-рациональных функций
1. \[ \int \frac{dx}{x^2-x}. \] 2. \[ \int \frac{dx}{(2x+3)^2}. \] 3. \[ \int \frac{dx}{2x^2-2x+3}. \] 4. \[ \int \frac{(x^2+2)dx}{x^3+x^2-2x}. \] 5. \[ \int \frac{dx}{x^3+x^2+2x+2}. \] 6. \[ \int \frac{x^2dx}{x^2-4x+3}. \] 7. \[ \int \frac{xdx}{(x+1)(2x-1)}. \] 8. \[ \int \frac{x^5+x^4-8}{x^3-4x}dx. \] 9. \[ \int \frac{dx}{(x^2+1)(x^2+4)}. \] 10. \[ \int \frac{dx}{(x-2)^2(x+2)^2}. \] 11. \[ \int \frac{dx}{x^4-1}. \]
Интегралы от тригонометрических функций
Вычислить первообразные
1. \[ \int \sin 2x\cos 5xdx. \] 2. \[ \int \sin ^2x\cos ^2xdx. \] 3. \[ \int \sin (3x+4) \sin (4x-1)dx. \] 4. \[ \int \frac{\cos 3x}{4+3\sin 3x}dx. \] 5. \[ \int \frac{\cos x}{1+\cos x}dx. \] 6. \[ \int \frac{\sin x}{\cos ^5x}dx. \] 7. \[ \int \frac{dx}{\sin^2x\cos ^4x}. \] 8. \[ \int \frac{1}{1+\cos x+\sin x}dx. \] 9. \[ \int \frac{\sin (2x)dx}{1+\sin ^2x}. \] 10. \[ \int \frac{dx}{\sin x(2\cos ^2x-1)}. \] 11. \[ \int \frac{dx}{5+3\cos x+4\sin x}. \] 12. \[ \int \frac{dx}{\cos x+3tg x}. \]
Интегралы от функций, содержащих иррациональности
Вычислить первообразные.
1. \[ \int \sqrt[3]{x}(\sqrt{x}+1)^3\,dx. \] 2. \[ \int \frac{1}{1+\sqrt[3]{x+1}}\,dx. \] 3. \[ \int \frac{1}{\sqrt{x+3}+\sqrt[3]{(x+3)^2}}\,dx. \] 4. \[ \int \frac{x^2+\sqrt{x+1}}{\sqrt[3]{x+1}}\,dx. \] 5. \[ \int \frac{\sqrt{x+5}}{\sqrt[3]{x+5}+1}\,dx. \] 6. \[ \int \frac{dx}{\sqrt{x}+\sqrt[3]{x}+2\sqrt[4]{x}}. \] 7. \[ \int x\sqrt{\frac{x-1}{x+1}}\,dx. \]Подстановки Эйлера
Вычислить первообразные.
1. \[ \int \sqrt{\frac{1-x}{1+x}}dx. \] 2. \[ \int \frac{dx}{x\sqrt{x^2+x+1}}. \] 3. \[ \int \frac{1}{x+\sqrt{1+x+x^2}}dx. \] 4. \[ \int \frac{1}{1+\sqrt{2+x+x^2}}dx. \] 5. \[ \int \frac{dx}{x\sqrt{2+x-x^2}}. \] 6. \[ \int \frac{dx}{x\sqrt{x^2+4x-4}}. \]Формула Ньютона-Лейбница
Вычислить интегралы<
1. \[ \int _{0}^1\sqrt{1+x}\,dx. \] 2. \[ \int _{-2}^{-1}\frac{dx}{(7+3x)^2}. \] 3. \[ \int _{2}^{-6}\frac{dx}{\sqrt[3]{(3-x)^2}}. \] 4. \[ \int _{0}^{16}\frac{dx}{\sqrt{x+9}-\sqrt{x}}. \] 5. \[ \int _{-a}^0\frac{(a+x)^2}{a}\,dx. \] 6. \[ \int _{0}^{\pi /2}\sin x \cos3x\, dx. \] 7. \[ \int _{0}^{\pi /4}\frac{dx}{\cos ^4x}. \] 8. \[ \int _{0}^{1/4}\frac{dx}{\sqrt{x-x^2}}. \] 9. \[ \int _{0}^{13}\frac{x+1}{\sqrt[3]{2x+1}}dx. \] 10. \[ \int _{ln2}^{ln3}\frac{e^{2x}}{e^x-e^{-x}}dx. \]
Признаки сходимости несобственных интегралов 1 рода
Вычислить несобственный интеграл или установить его сходимость(расходимость)
1. \[ \int _{0}^{+\infty}e^{-ax}\,dx. \] 2. \[ \int _{0}^{+\infty}xe^{-x^2}\,dx. \] 3. \[ \int _{-\infty}^{+\infty}\frac{2xdx}{x^2+1}. \] 4. \[ \int _{0}^{+\infty}\frac{xdx}{(x+2)^3}. \] 5. \[ \int _{-\infty}^{+\infty}\frac{dx}{x^2+2x+2}. \] 6. \[ \int _{1}^{+\infty}\frac{lnx}{x^2}\,dx. \] 7. \[ \int _{1}^{+\infty}\frac{dx}{(1+x)\sqrt{x}}. \] 8. \[ \int _{0}^{+\infty}e^{-\sqrt{x}}\,dx. \] 9. \[ \int _{0}^{+\infty}e^{-ax}\cos x\,dx. \] 10. \[ \int _{0}^{+\infty}\frac{xdx}{x^3+1}. \]Признаки сходимости несобственных интегралов 2 рода
Вычислить несобственный интеграл или установить его сходимость(расходимость)
1. \[ \int _{0}^{1}\frac{dx}{x^3-5x^2}\,. \] 2. \[ \int _{3}^{7}\frac{x\,dx}{(x-5)^2}\,. \] 3. \[ \int _{0}^{1}\frac{x\,dx}{\sqrt{1-x^2}}\,. \] 4. \[ \int _{0}^{1}\frac{x^3\,dx}{1-x^5}\,. \] 5. \[ \int _{-3}^{2}\frac{dx}{(x+3)^2}\,. \] 6. \[ \int _{1}^{2}\frac{x^2\,dx}{(x-1)\sqrt{x-1}}\,. \] 7. \[ \int _{0}^{1}\frac{dx}{\sqrt{x+x^2}}\,. \] 8. \[ \int _{0}^{1/4}\frac{dx}{\sqrt{x-x^2}}\,. \] 9. \[ \int _{1}^{2}\frac{dx}{xlnx}\,. \] 10. \[ \int _{1}^{2}\frac{x^3\,dx}{\sqrt{4-x^2}}\,. \] 11. \[ \int _{0}^{\pi /4}\frac{dx}{\sin ^4x}\,. \]Площадь плоских фигур
1. Найти площадь, ограниченную кривыми $y=x^2-4$ и $x-y+8=0$.
2. Найти площадь, ограниченную кривыми $xy=2$ и $x+2y=5$.
3. Найти площадь, ограниченную кривыми $y=e^x, \quad y=e^{-x}, \quad x=1$.
4. Найти площадь, ограниченную кривыми $y^2=3x, \quad x^2=3y$.
5. Найти площадь, ограниченную кривыми $x^2=4y, \quad y=8/(x^2+4)$.
6. Найти площадь, ограниченную кривой $r=a\sin (3\varphi )$.
7.
Найти площадь, ограниченную кривой $x=3(t-\sin t), \quad y=3(1-\cos t)$, где $0 8.
Найти площадь, ограниченную кривой $(x^2+y^2)^5=a^6x^3y$. 9.
Найти площадь, ограниченную кривыми $r=2(1-\cos \varphi ), \quad r=\varphi $, $ 0 \leq \varphi \leq 2\pi$.
Длина дуги кривой
1. Найти длину дуги кривой $y=ln(1-x^2)$ от $x=0$ до $x=1/2$.
2. Найти длину дуги кривой $y^2=(1+x)^3$ от $x=0$ до $x=3$.
3. Найти длину дуги астроиды $y=2\sin ^3t, \quad x=2\cos ^3t$.
4. Найти длину дуги кардиоиды $r=3(1-\cos \varphi)$.
5. Найти длину первого витка спирали Архимеда $r=a\varphi, \quad a>0$.
Вычисление объма тел
1. Вычислить объем тела, образованного вращением вокруг оси $x$ фигуры, ограниченной параболами $y=x^2$ и $y^2=x$. $y=ln(1-x^2)$ от $x=0$ до $x=1/2$.
2. Вычислить объем тела, образованного вращением вокруг оси $y$ фигуры, ограниченной параболами $y=x^2$ и $y=2-x^2$.
3. Вычислить объем тела, образованного вращением вокруг оси $x$ фигуры, ограниченной кривыми $y=(1+x^2)^{-1}$, $y=x/2$ и $x=0$.
4. Вычислить объем тела, образованного вращением вокруг оси $x$ кривой $y=\sin x$, $0 \leq x \leq \pi$.
5. Вычислить объем тела, образованного вращением вокруг оси $y$ фигуры, ограниченной параболами $y=2x-x^2$ и $y=0$.
Приложения в механике
1. Найти кооординаты центра масс (полагая распределение масс равномерным)
а) симметричного параболического сегмента с основанием $a$ и высоты $h$;
б) дуги окружности радиуса $R$, стягивающей центральный угол $\alpha $.
2. Найти момент инерции (полагая распределение масс равномерным)
а) полукруга радиуса $R$ относительно его диаметра;
б) конуса с радиусом основания $R$, высоты $H$, относительно его оси;
в) шара радиуса $R$ относительно его диаметра.