4. Аналитическая геометрия в трехмерном пространстве

4.4 Прямая в трехмерном пространстве

4.3 Пл-ть в трехмерном пространстве 4.5 Взаимное расположение прямой и пл-ти в трехмерном пространстве

Фиксировать прямую в трехмерном пространстве можно, задавая точку $M_0$, через которую проходит прямая, и направляющий вектор прямой $\textbf {a}$. Пусть точке $M_0$ соответствует вектор $ \textbf {r}_0$, текущей точке прямой $M$ соответствует вектор $\textbf {r}$, тогда вектора $\textbf {r}-\textbf {r}_0$ и $\textbf {a}=(a_1,\, a_2, \,a_3)^T$ отличаются только множителем, \begin{equation} \textbf {r}-\textbf {r}_0=\textbf {a}t. (36) \label{pryam_3} \end{equation} Это уравнение называется векторным уравнением прямой, см. рис. \ref{pryam33}. Когда параметр $t$ пробегает значения от $-\infty$ до $\infty$, точка $M$ пробегает прямую.

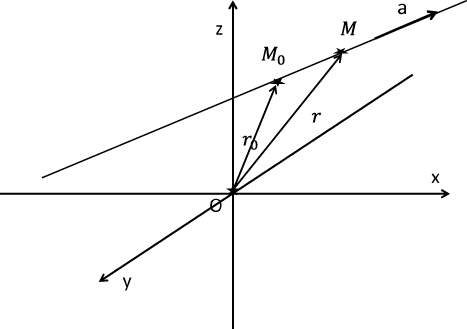
Рис 15: Прямая в трехмерном пространстве задается фиксированной точкой $M_0$ и направляющим вектором $\textbf {a}$.

Записывая это уравнение в координатах, получаем: \[ x-x_0=a_1t, \quad y-y_0=a_2t, \quad z-z_0=a_3t. \] Этот набор уравнений называется параметрическим описанием прямой в трехмерном пространстве. Исключая $t$ из этих уравнений, находим: \begin{equation} \frac{x-x_0}{a_1}=\frac{y-y_0}{a_2}=\frac{z-z_0}{a_3}. (37) \label{pryam31} \end{equation} Эти уравнения называются координатными уравнениями прямой. Заметим, что по знаменателям в этом соотношении можно восстановить вектор $\textbf {a}=(a_1,\, a_2, \,a_3)^T$. Выпишем уравнение прямой, проходящей через две заданные точки, $M_0=(x_0,\, y_0, \,z_0)$, $M_1=(x_1,\, y_1, \,z_1)$. Подставляя вторую точку в уравнение (37) и затем разделив (37) на результат подстановки, получим искомое уравнение: \begin{equation} \frac{x-x_0}{x_1-x_0}=\frac{y-y_0}{y_1-y_0}=\frac{z-z_0}{z_1-z_0}. (38) \label{pryam32} \end{equation} Далее, в трехмерном пространстве прямую можно представить как результат пересечения двух плоскостей, т.е. как результат совместного решения уравнений \begin{equation} A_1x+B_1y+C_1z+D_1=0, \quad A_2x+B_2y+C_2z+D_2=0. (39) \label{pryam34} \end{equation} Заметим, что уравнения прямой (37), (38) можно трактовать как уравнения вида (39).

Пример.

Контрольный вопрос.

Решение типовых задач.

Задачи.

4.3 Пл-ть в трехмерном пространстве 4.5 Взаимное расположение прямой и пл-ти в трехмерном пространстве