3. Аналитическая геометрия на плоскости
3.5 Эллипс
Выпишем еще раз каноническое уравнение эллипса,
\begin{equation}
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,
\label{ell1}
\end{equation}
см. соответствующий рисунок 5.
При каноническом описании полагают, что $a>b>0$. Заметим, что если $a=b$, то эллипс превращается в окружность. Точки $(a,0), \, (-a,0), \, (0, b),\, (0, -b)$ называют вершинами эллипса, параметр $a$ - большая полуось, параметр $b$ - малая полуось. Далее, вводят параметр $c=\sqrt{a^2-b^2}$, точки $(c,0), \, (-c,0)$ называют фокусами эллипса. Величину $\varepsilon = c/a$ называют эксцентриситетом эллипса. Она характеризует вытянутость эллипса. Из определений следует, что для эллипса $0 \leq \varepsilon \leq 1$.
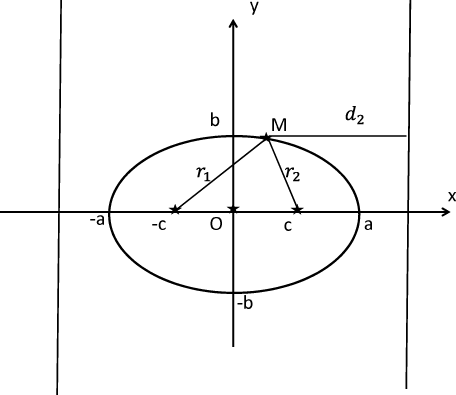
Рис 5: Эллипс и его директрисы.
Опишем сначала элементарные свойства эллипса, следующие непосредственно из канонического уравнения (19).
1. Из этого уравнения следует, что если точка $(x,y)$ принадлежит эллипсу, то выполняются неравенства $|x| \leq a $, $|y| \leq b$. Таким образом, все точки эллипса лежат в этом прямоугольнике (конечном!).
2. Так как переменные $x,y$ входят в уравнение эллипса только в квадратах, то из того, что $(x,y)$ лежат на эллипсе следует, что точки $(\pm x, \, \pm y)$ также лежат на эллипсе при любом выборе знаков. Это означает, что эллипс симметричен при отражении относительной осей координат и имеет центр симметрии, точку $O$.
Эллипс можно описать как геометрическое место точек. Для этого соединим точку $M$, лежащую на эллипсе, с фокусами. Соответствующие отрезки называются фокальными радиусами точки (см. рис. 5, отрезки $r_1, \, r_2$).
Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее фокальных радиусов равнялась $2a$,
\begin{equation}
r_1+r_2=2a.
\label{ell2}
\end{equation}
Доказательство.
1. Достаточность. Из рисунка получаем:
\[
r_1=\sqrt{(x+c)^2+y^2}, \quad r_2=\sqrt{(x-c)^2+y^2},
\]
так что выполняется условие
\[
\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2a.
\]
Покажем, что отсюда следует, что $(x,y)$ удовлетворяет уравнению (19). Надо избавиться от корней. Для этого перенесем один из корней направо и возведем в квадрат. Раскрывая скобки, получаем:
\[
x^2+2xc+c^2+y^2=4a^2-4a\sqrt{(x-c)^2+y^2}+x^2-2xc+c^2+y^2.
\]
Сокращая подобные члены и деля на 4, получаем:
\[
a\sqrt{(x-c)^2+y^2}=a^2-xc.
\]
Возводя еще раз в квадрат, приходим к формуле:
\[
a^2(x^2-2xc+c^2+y^2)=a^4-2a^2xc+x^2c^2.
\]
Сокращая еще раз подобные члены, получаем:
\[
(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2).
\]
Подставляя $c^2=a^2-b^2$, получаем соотношение, только множителем отличающееся от соотношения (19).
2. Необходимость. Пусть выполняется (19), вычислим $r_1$. Имеем:
\[
r_1=\sqrt{(x+c)^2+y^2}=\sqrt{(x+c)^2+b^2-\frac{b^2x^2}{a^2}}=
\]
\[
\sqrt{x^2+2xc+c^2+b^2-\frac{b^2x^2}{a^2}}=\sqrt{\frac{c^2x^2}{a^2}+2xc+a^2}=a+\varepsilon x.
\]
Вычисление $r_2$ по этой схеме приводит к результату (имеется отличие только в одном знаке!) $r_2=a-\varepsilon x$, из свойств эллипса следует, что в правой части - положительное число. Складывая, получаем (20). ч.т.д.
Имеется еще одно описание эллипса. Введем т.н. директрисы эллипса - прямые $x=\pm a/\varepsilon$, см. рис. 2.
Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния от этой точки до фокуса к расстоянию до соответствующей директрисы было равно эксцентриситету эллипса,
\begin{equation}
r_2/d_2=\varepsilon. (21)
\label{ell3}
\end{equation}
Доказательство.
1. Достаточность. Пусть $r_2=\varepsilon d_2$. Из рисунка следует, что $d_2=a/ \varepsilon -x$, так что
\[
\sqrt{(x-c)^2+y^2}=a-\varepsilon x.
\]
Возводя в квадрат, получаем:
\[
x^2+2xc+c^2+y^2=a^2+2\varepsilon x+\varepsilon ^2x^2.
\]
Приводя подобные члены и учитывая явное выражение для $\varepsilon $, получаем:
\[
\frac{b^2x^2}{a^2}+y^2=b^2.
\]
Это соотношение, после домножения на подходящий множитель, переходит в (19).
2. Необходимость. Пусть точка $(x,y)$ лежит на эллипсе, т.е. выполняется уравнение (19). Как было показано при доказательстве предыдущей теоремы, мы получаем $r_2=a-\varepsilon x$. Из рисунка: $d_2=a / \varepsilon -x$. Делим одно на другое - получаем (21). ч.т.д.
Пример.
Пусть известно следующее: расстояния одного из фокусов эллипса до концов большой оси равны 7 и 1. Составим уравнение этого эллипса. Указанные расстояния равны $a+c$ и $a-c$ соответственно, так что имеем: $a=4$, $c=3$. Далее, $c=\sqrt{a^2-b^2}$, откуда $b=\sqrt{16-9}=\sqrt{7}$. В итоге получаем уравнение эллипса:
\[
\frac{x^2}{16}+\frac{y^2}{7}=1.
\]
Решение типовых задач.
Задача 1.
Дано уравнение эллипса $x^2+4y^2=25$. Вычислить длину его полуосей, координаты фокусов и эксцентриситет.
Решение.
Приведем уравнение эллипса к каноническому виду:
\[
\frac{x^2}{25}+\frac{4y^2}{25}=1
\]
или
\[
\frac{x^2}{5^2}+\frac{y^2}{(\frac{5}{2})^2}=1
\]
Отсюда получим, что длина большой полуоси $a=5$, длина малой полуоси $b=\frac{5}{2}$.
Найдем параметр $c$:
\[
c=\sqrt{a^2-b^2}=\sqrt{5^2-\left(\frac{5}{2}\right)^2}=\frac{5}{2}\sqrt{3}.
\]
Тогда точки фокуса имеют координаты $\left(-\frac{5}{2}\sqrt{3},0 \right)$ и $\left( \frac{5}{2}\sqrt{3},0 \right)$ .
Эксцентриситет равен $\varepsilon = \frac{c}{a}=\frac{\frac{5}{2}}{5} = \frac{1}{2}$.
Задача 2.
Написать уравнение эллипса с фокусами $C_1(-7;0)$ и $C_2 (7;0)$, проходящего через точку $\textbf {M}(-2;12)$.
Решение.
Найдем фокальные радиусы точки $\textbf {M}$:
\[
r_1 = |MC_1| = \sqrt{(-7-(-2))^2+(0-12)^2}=13,
\]
\[
r_2 = |MC_2| = \sqrt{(7-(-2))^2+(0-12)^2}=15.
\]
Согласно приведенной выше теореме, сумма фокальных радиусов равна длине большой оси эллипса: $r_1+r_2=2a$, следовательно, в нашем случае имеем $13+15=2a$. Значит длина большой полуоси $a=14$.
Длину малой полуоси найдем из равенства $c=\sqrt{a^2-b^2}$. Тогда
\[
b=\sqrt{a^2-c^2}=\sqrt{14^2-7^2}= 7 \sqrt{3}.
\]
Таким образом, каноническое уравнение эллипса с заданными условиями есть
\[
\frac{x^2}{196}+\frac{y^2}{147}=1
\]
Задача 3.
В эллипс $\frac{x^2}{49}+\frac{y^2}{24}=1$ вписан прямоугольник, две противоположные стороны которого проходят через фокусы. Вычислить площадь этого прямоугольника.
Решение.
Исходя из условия, можно утверждать, что одна из сторон вписанного в эллипс прямоугольника равна $2c$, где $c=\sqrt{a^2-b^2}=\sqrt{49-24}=5$.
Длина другой стороны есть длина хорды, перпендикулярной оси абсцисс и проходящей через фокус эллипса, т.е. соответсвующей уравнению $x=5$. Подставив в уравнение эллипса $x=5$, получим
\[
\frac{5^2}{49}+\frac{y^2}{24}=1
\]
Отсюда $y^2=\frac{24^2}{49}$, тогда $y=\pm \frac{24}{7}$.
Вторая сторона прямоугольника равна $2|y|$.
Тогда искомая площадь равна
\[
S=2c \cdot 2|y| = 10 \cdot \frac{48}{7} = 68 \frac{4}{7}.
\]
Задачи.
1. Дано уравнение эллипса $25x^2+169y^2=4225$. Вычислить длину его осей, координаты фокусов и эксцентриситет.
2. Составить простейшее уравнение эллипса, у которого сумма полуосей и расстояние между фокусами равны 8.
3. В эллипс
\[
\frac{x^2}{49}+\frac{y^2}{24}=1
\]
вписан прямоугольник, противоположные стороны которого проходят через фокусы. Вычислить его площадь.
4. На эллипсе
\[
\frac{x^2}{30}+\frac{9y^2}{24}=1
\]
найти точку, расстояние которой от оси $y$ равно пяти.
5. Эллипс, оси которого совпадают с осями координат, проходит через точки $М(2, 30.5)$ и $N(0, 2)$. Написать его уравнение и найти фокальные радиусы точки М.
6. Составить простейшее уравнение эллипса, проходящего через точки $M(\sqrt{3}, -2)$ и $N(-2\sqrt{3},1)$.
7. Написать уравнение эллипса, если расстояние между директрисами равно 12, а большая полуось равна $2\sqrt{3}$.
8. В эллипс
\[
\frac{x^2}{36}+\frac{y^2}{9}=1
\]
вписан правильный треугольник, одна из вершин которого совпадает с правой вершиной большой оси. Найти координаты двух других вершин треугольника.
9. На эллипсе
\[
\frac{x^2}{100}+\frac{y^2}{36}=1
\]
найти точку, расстояние которой от правого фокуса в 4 раза больше расстояния от левого фокуса.
10. Дан эллипс
\[
\frac{x^2}{9}+\frac{y^2}{4}=1.
\]
Через точку $(1,1)$ провести хорду, делящуюся в этой точке пополам.