3. Аналитическая геометрия на плоскости
3.4 Прямая на плоскости
Для прямой на плоскости мы приведем несколько уравнений. В зависимости от задачи удобнее использовать то или иное уравнение и довольно часто требуется перейти от уравнения прямой в одной форме к уравнению, описывающему прямую в другой форме.
Для того, чтобы фиксировать прямую на плоскости, достаточно указать точку, через которую она проходит (точку $M_0$) и направление - направляющий вектор $\textbf {a}$, лежащий на плоскости. Соединяя с точкой $O$ точку $M_0$ и текущую точку прямой $M$, получаем пару векторов $ \textbf {r}_0$, $ \textbf {r}$, см. рис. 3. Тогда вектор $\textbf {r} - \textbf {r}_0$ лишь длиной отличается от вектора $\textbf {a}$. Записывая этот факт, получаем векторное уравнение прямой:
\begin{equation}
\textbf {r} - \textbf {r}_0=t\cdot \textbf {a}. (13)
\label{pryam1}
\end{equation}
Здесь число $t$ имеет смысл коэффициента пропорциональности между векторами $\textbf {r} - \textbf {r}_0$ и $\textbf {a}$. Когда точка $M$ пробегает прямую, параметр $t$ пробегает значения от $-\infty$ до $+\infty$.
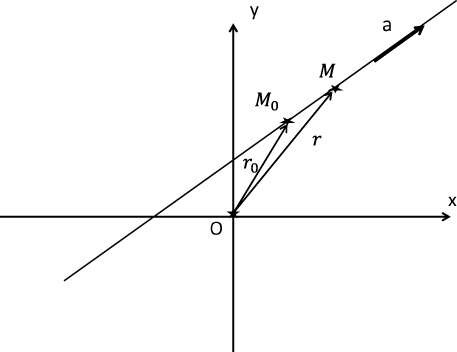
Рис 3: Прямая определяется точкой, через которую она проходит, и направляющим вектором.
Если $(a_1,\,a_2)$ - координаты вектора $\textbf {a}$, $(x,y)$ - координаты вектора $\textbf {r} $, $(x_0,y_0)$ - координаты вектора $\textbf {r}_0 $, то уравнение (13) можно записать покоординатно,
\begin{equation}
x=x_0+a_1t, \quad
y=y_0+a_2t. (14)
\label{pryam2}
\end{equation}
Эту пару уравнений называют параметрическим представлением прямой на плоскости. Исключая параметр $t$ из этой пары уравнений, получим:
\begin{equation}
y-y_0=k(x-x_0), \quad k=a_2/a_1. (15)
\label{pryam3}
\end{equation}
Это уравнение называется уравнением прямой с угловым коэффициентом, проходящей через заданную точку. Его можно переписать в виде:
\begin{equation}
y=kx+b, \quad b=y_0-kx_0. (16)
\label{pryam4}
\end{equation}
Это уравнение называется уравнением прямой с угловым коэффициентом. Геометрический смысл $k$ устанавливается, если продифференцировать функцию $y(x)$ по $x$ - $k=tg \alpha$, где $\alpha $ - угол между прямой и положительным направлением оси $x$. Величина $b$ определяет величину отрезка, отсекаемого прямой на оси $y$, см. рис. 4.
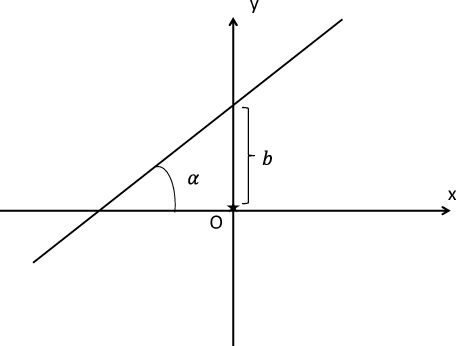
Рис 4: Прямая: фиксирован угловой коэффициент и отрезок, отсекаемый на оси $y$.
Далее, нетрудно из уравнения (15) вывести уравнение прямой, проходящей через 2 заданные точки. В самом деле, если прямая проходит через точки $(x_0, \, y_0)$ и $(x_1, \, y_1)$, то, подставляя вторую точку в уравнение (15) находим значение $k$, так что в итоге уравнение прямой приобретает вид:
\begin{equation}
\frac{y-y_0}{y_1-y_0}=\frac{x-x_0}{x_1-x_0}. (17)
\label{pryam5}
\end{equation}
Имеется еще одно полезное при решении ряда задач уравнение прямой, т.н. нормальное уравнение прямой. Пусть $\textbf {a}=(a-1,\, a_2)$ - направляющий вектор прямой на плоскости. Тогда нетрудно построить нормаль $\textbf {N}$ к этому вектору, вектор, ортогональный $\textbf {a}$ и поэтому ортогональный прямой, $\textbf {N}=(a_2, \, -a_1)$. Выпишем условие ортогональности векторов $\textbf {r} - \textbf {r}_0$ и $\textbf {N}$:
\[
(\textbf {r} - \textbf {r}_0, \textbf {N})=0.
\]
Подставим в это уравнение вместо вектора $\textbf {N}$ вектор единичной длины, совпадающий с ним по направлению, $\textbf {n}=\textbf {N}/|\textbf {N}|$. Полагая $\textbf {n}=(\cos \beta, \sin \beta)$, получим уравнение
\begin{equation}
x\cos \beta+y \sin \beta=d. (18)
\label{pryam6}
\end{equation}
При этом параметр $\beta $ имеет смысл угла, который образует прямая с осью $y$, а модуль $d$ равен расстоянию от прямой до начала координат.
Последнее уравнение прямой - т.н. общее уравнение прямой на плоскости,
\[
Ax+By+C=0.
\]
Очевидно, что любое из предыдущих уравнений может быть записано в этом виде.
Угол между двумя прямыми можно вычислить разными способами, в зависимости от вида уравнений, которыми заданы прямые. Если они заданы векторными уравнениями, то этот угол равен углу между направляющими векторами прямых $\textbf {a}_1 ,\, \textbf {a}_2$, так что
\[
\cos \phi =\frac{(\textbf {a}_1 ,\, \textbf {a}_2)}{|\textbf {a}_1 | \cdot | \textbf {a}_2|}.
\]
Пусть прямые заданы уравнениями с угловыми коэффициентами вида (16), которые имеют смысл тангенса угла наклона прямых к оси $x$. Вспоминая формулу для тангенса разности углов, можно написать для угла $ \phi$ между прямыми:
\[
tg \phi =\frac{k_1-k_2}{1+k_1\cdot k_2}.
\]
Отсюда условие параллельности прямых: $k_1=k_2$, условие ортогональности прямых: $k_1\cdot k_2=-1$ (в этом случае знаменатель последнего соотношения обращается в 0).
Приведем еще пару полезных формул, которые нетрудно вывести из уравнений прямой. Расстояние от заданной точки $(x_1,y_1)$ до прямой $Ax+By+C=0$ вычисляется по формуле
\[
p=\frac{Ax_1+By_1+C}{\sqrt{A^2+B^2}}.
\]
Длина отрезка $MN$, $M=(x_1,y_1)$, $N=(x_2,y_2)$, вычисляется по формуле
\[
L=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}.
\]
Пример.
Проведем через точку $(-1,\,1)$ прямую, параллельную прямой $2x+3y+7=0$. Эта прямая будет иметь уравнение $2x+3y+C=0$, где число $C$ подлежит определению (коэффициенты перед $x,\,y$ определяют наклон прямой и если мы возьмем их, как в исходной прямой, получим параллельную прямую). Подставляя точку в искомую прямую, получим уравнение для $C$: $-2+3+C=0$, так что $C=-1$ и искомое уравнение прямой: $2x+3y-1=0$.
Контрольный вопрос.
Пусть задано общее уравнение прямой на плоскости. Перепишите его в виде нормального уравнения прямой.
Решение типовых задач.
Задача 1.
Написать уравнения прямой в общем виде и с угловым коэффициентом, если прямая проходит через точки $\textbf {А}(2,3)$ и $\textbf {B}(4,-6)$.
Решение.
Для написания уравнения искомой прямой воспользуемся формулой (\ref{pryam5}). Подставляя в нее вместо $(x_0,y_0)$ координаты точки $\textbf {А}$, а вместо $(x_1,y_1)$ - координаты точки $\textbf {B}$, получим
\[
\frac{y-3}{(-6)-3}=\frac{x-2}{4-2}.
\]
или
\[
\frac{y-3}{-9}=\frac{x-2}{2}.
\]
С помощью несложных элементарных преобразований (домножения на наименьший общий знаменатель, переноса в левую часть и приведения подобных слагаемых), получим уравнение в общем виде:
\[
2y + 9x -24 = 0
\]
Теперь приведем это уравнение к виду уравнения прямой с угловым коэффициентом:
\[
y = 12 - \frac{9x}{2}.
\]
Задача 2.
Две стороны параллелограмма заданы уравнениями $2x+5y+6=0$ и $x-3y=0$. Известны координаты одной из вершин параллелограмма - $\textbf {K}(4;-1)$. Написать уравнения двух других сторон параллелограмма.
Решение.
В параллелограмме противоположные стороны параллельны, значит исходная задача сводится к построению прямых, параллельных данным и проходящих через заданную точку.
Построим прямую, параллельную прямой $2x+5y+6=0$. Ее уравнение будет иметь вид $2x+5y+C=0$. Значение $\textbf {С}$ определим, подставив в это уравнение координаты точки $\textbf {K}$: $2 \cdot 4 + 5 \cdot (-1) + C=0$. Следовательно, $\textbf {С = -3}$ и искомое уравнение стороны есть
\[
2x+5y-3=0
\]
Аналогичным образом, подставляя в уравнение $x-3y+C=0$ координаты точки $\textbf {K}$: $4 -3 \cdot (-1)+C=0$, получим уравнение другой стороны параллелограмма:
\[
x-3y-7=0.
\]
Задача 3.
Проверить, что прямые
\[
y = 3x-1, x+y-7=0, x-7y=7
\]
служат сторонами равнобедренного треугольника.
Решение.
Известно, что равнобедренным называется треугольник, две стороны которого имеют равную длину. Следовательно, наша задача сводится к нахождению точек пересечения заданных прямых и длин соответствующих сторон треугольника.
Найдем точку пересечения прямых $y = 3x-1, x+y-7=0$, решив систему из этих уравнений. Получим точку \textbf {A} (2,5).
Аналогично, решив систему из уравнений $y = 3x-1, x-7y=7$, получим координаты другой вершины - \textbf {B} (0,-1).
Наконец, решение системы $x+y-7=0, x-7y=7$ есть координаты точки пересечения этих прямых, т.е. координаты третьей вершины - \textbf {C} (7,0).
Найдем длины сторон треугольника, т.е. длины отрезков \textbf {AB}, \textbf {AC}, \textbf {BC}:
\[
|AB|=\sqrt{(0-2)^2+(-1-5)^2} = \sqrt{40},
|AC|=\sqrt{(7-2)^2+(0-5)^2} = \sqrt{50},
\]
\[
|BC|=\sqrt{(7-0)^2+(0-(-1))^2} = \sqrt{50}.
\]
Мы получили, что $|AC|=|BC|$, значит, действительно, исходные прямые задают стороны равнобедренного треугольника.
Задача 4.
Выяснить являются ли перпендикулярными прямые $3x-2y=0$ и $-4x-6y+3=0$.
Решение.
Приведем уравнения к виду уравнений с угловыми коэффициентами:
\[
y = \frac{3x}{2}, y = -\frac{2x}{3}+\frac{1}{2}
\]
Тогда угловой коэффициент первого уравнения $k_1=\frac{3}{2}$, второго - $k_1=-\frac{2}{3}$. Проверим условие ортогональности, согласно которому
$k_1\cdot k_2=-1$. В нашем случае имеем $k_1\cdot k_2=\frac{3}{2}\cdot -\frac{2}{3}= -1$ . Это означает, что заданные прямые перпендикулярны.
Задача 5.
Найти расстояние от прямой $\frac{x+3}{-4}=\frac{y-2}{3}$ до точки $P(2,-1)$.
Решение.
Приводя исходное уравнение к общему виду, получим
\[
3x+4y+1 =0.
\]
Расстояние от точки $P(2,-1)$ до прямой вычислим по формуле
\[
p=\frac{\left | 3\cdot 2 + 4 \cdot (-1) + 1 \right |}{\sqrt{3^2+4^2}} =
\frac{2}{5}.
\]
Задачи.
1. Составить уравнение прямой, проходящей через точку $ M(-2,1)$ и параллельной прямой
\[
\frac{x+7}{-5}=\frac{y+9}{-4}.
\]
2. Составить уравнение прямой, проходящей через точку $M(-2,1)$ и перпендикулярной прямой
\[
\frac{x+7}{-5}=\frac{y+9}{-4}.
\]
3. Найти угол между прямыми
\[
\frac{x+7}{5}=\frac{y+3}{4}, \quad \frac{x+2}{4}=\frac{y-2}{-5}.
\]
4. Составить уравнение биссектрисы острого угла между прямыми $3y=4x$ и $5x+12y=6$.
5. Написать уравнение прямой, удаленной на 5 от прямой $12x+5y=39$.
6. Основания трапеции лежат на прямых
\[
2x+\sqrt{5}y-24=0, \quad 2x+\sqrt{5}y+6=0.
\]
Найти ее высоту.
7. Проверить, что прямые $2x+\frac{11}{2}y-15=0$ и $\frac{23}{2}x-5y+30=0$ касаются одной и той же окружности с центром в начале координат и вычислить ее радиус.
8. На расстоянии 5 от точки $M(4,3)$ провести прямую, отсекающую равные отрезки на осях координат.
9. На оси $y$ найти точку, равноудаленную от начала координат и от прямой $3x-4y=12=0$.
10. Через точку пересечения прямых $2x-y=2$ и $x+y=1$ провести прямую, параллельную прямой $y=3x-2$.
11. Составить уравнения катетов прямоугольного равнобедренного треугольника, зная уравнение гипотенузы $y=3x+5$ и вершину прямого угла $M(4,-1)$.
12. Вычислить координаты вершин ромба, если известны уравнения двух его сторон $2x-5y-1=0$ и $2x-5y-34=0$ и уравнение одной из диагоналей $x+3y-6=0$.
13. Найти уравнения сторон треугольника, зная одну из его вершин $A(3,4)$ и уравнения двух высот $7x-2y=1$ и $2x-7y=6$.
14. Через точку $M(0,1)$ провести прямую так, чтобы ее отрезок, заключенный между двумя данными прямыми $x-3y+10$ и $2x+y-8=0$, делился в этой точке пополам.
15. Составить уравнения сторон треугольника, зная одну из его вершин $A(-4,2)$ и уравнения двух медиан $3x-2y+2=0$ и $3x+5y-12=0$.
16. Даны две противоположные вершины квадрата $A(-5,2)$ и $C(3,-4)$. Составить уравнения его сторон.