4. Производная, дифференциальное исчисление

4.1.1 Определение производной

Понятие производной - одно из ключевых в математическом анализе. Пусть $f(x)$ задана на некотором интервале $(a,b) \subset\mathbb{R}$, точка $x_0 \in (a,b)$.

Рассмотрим отношение \[ A(x_0, \vartriangle x)=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x }. \]

Это функция двух переменных - $x_0$ и еще одной переменной, которую обозначают $ \Delta x$. Числитель этой дроби обозначают иногда как $\Delta f=f(x_0+\Delta x)-f(x_0)$ и называют приращением функции $f(x)$ в точке $x_0$, соответствующим приращению аргумента $\Delta x$, так что \[ A(x_0, \Delta x)=\frac{\Delta f}{\Delta x }. \]

Определение. Если существует конечный предел \[ \lim _{\Delta \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x }=k, \] то говорят, что функция $f(x)$ дифференцируема в точке $x=x_0$, имеет там производную, равную $k$, которую обозначают $\frac{df}{dx}(x_0)$ или $f'(x_0)$.

Итак, если $f(x)$ дифференцируема в точке $x=x_0$, то \[ \frac{df}{dx}(x_0)=f'(x_0)=\lim _{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x }. \]

Можно получить определение левой производной, если допускать лишь отрицательные значения $ \Delta x$, и правой производной, допуская лишь положительные значения $ \Delta x$.

Примеры.

Замечание. В точках разрыва функции $f(x)$ функция не имеет производной.

Контрольный вопрос.

Первые физические приложения.

1. Путь $S(t)$ - путь, пройденный движущейся по прямой точкой. Тогда мгновенной скоростью точки будет \[ v(t)=\lim _{\Delta t \to 0} \frac{S(t+\Delta t)-S(t)}{\Delta t}= \frac {dS}{dt}(t). \]

2. Пусть через данное сечение провода к моменту $t$ протек заряд $Q(t)$, тогда электрический ток \[ I(t)=\lim _{\Delta t \to 0} \frac{Q(t+\Delta t)-Q(t)}{\Delta t}= \frac {dQ}{dt}(t). \]

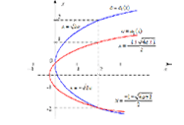
Обсудим геометрический смысл производной. На рисунке изображен график функции $y=f(x)$, проходящий через (близкие друг другу) точки $A$ и $B$. Проведем через них хорду $AB$. Отношение $(f(x+\Delta x)-f(x))/\Delta x$ соответствует тангенсу угла наклона хорды $AB$. Когда $\Delta x \rightarrow 0$, точка $B$ стремится к точке $A$, при этом хорда превращается в касательную к графику функции, проходящую через точку $(x,f(x))$. Соответственно, предел отношения превращается в тангенс угла наклона касательной. Итак, $f'(x)=tg \alpha $ - значение производной равно тангенсу угла наклона касательной к графику функции, проходящей через точку $(x,f(x))$.

Рис. 2: Геометрический смысл производной.

4.1.2 Производная от элементарных функций

Вычисление производных от элементарных функций сводится к вычислению пределов, причем мы используем замечательные пределы.

1. $f(x)=x^\alpha $, $f'(x)=\alpha \cdot x^{\alpha -1}.$ Частный случай $\alpha =0$: $f(x)=1$, $f'(x)=0$. Частный случай $\alpha =1$: $f(x)=x$, $f'(x)=1$.

Вычисление. Выписываем: \[ A(x_0, \Delta x)=\frac{(x_0+\Delta x)^{\alpha }-x_0^{\alpha }}{\Delta x}= \] \[ x_0^{\alpha }\frac{(1+\frac{\Delta x}{x_0})^{\alpha }-1}{\Delta x}= \] \[ x_0^{\alpha -1}\frac{(1+\frac{\Delta x}{x_0})^{\alpha }-1}{\frac{\Delta x}{x_0}}. \]

Используя степенной замечательный предел при $\Delta x/x_0 \rightarrow 0$, получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=\alpha x_0^{\alpha -1}. \]

2. $f(x)=e^x$, $f'(x)=e^x$.

Вычисление. В данном случае \[ A(x_0, \Delta x)=\frac{e^{x_0+\Delta x}-e^{x_0}}{\Delta x}=e^{x_0}\frac{e^{\Delta x}-1}{\Delta x}. \]

С помощью показательного замечательного предела получаем при $\Delta x \rightarrow 0$: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=e^{x_0}. \]

3. $f(x)=\sin x$, $f'(x)=\cos x$.

Вычисление. \[ A(x_0, \Delta x)=\frac{\sin (x_0+\Delta x)-\sin (x_0)}{\Delta x}. \]

Используя известное тригонометрическое тождество (разность синусов равна...), имеем: \[ A(x_0, \Delta x)=2\frac{\sin (\Delta x/2)\cos (x_0+\Delta x/2)}{\Delta x}= \] \[ \frac{\sin (\Delta x/2)\cos (x_0+\Delta x/2)}{\Delta x /2}. \]

С помощью тригонометрического предельного соотношения при $\Delta x \rightarrow 0$ получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=\cos (x_0). \]

4. $f(x)=\cos x$, $f'(x)=-\sin x$.

Вычисление. \[ A(x_0, \Delta x)=\frac{\cos (x_0+\Delta x)-\cos (x_0)}{\Delta x}. \]

Используя известное тригонометрическое тождество (разность косинусов равна...), имеем: \[ A(x_0, \Delta x)=-2\frac{\sin (\Delta x/2)\sin (x_0+\Delta x/2)}{\Delta x}= \] \[ -\frac{\sin (\Delta x/2)\sin (x_0+\Delta x/2)}{\Delta x /2} \]

С помощью тригонометрического предельного соотношения при $\Delta x \rightarrow 0$ получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=-\sin (x_0) \]

5. $f(x)=\ln x$, $f'(x)=1/ x$.

Вычисление. \[ A(x_0, \Delta x)=\frac{\ln (x_0+\Delta x)-\ln (x_0)}{\Delta x}= \] \[ \frac{\ln ((x_0+\Delta x)/x_0)}{\Delta x}=\frac{1}{x_0}\frac{\ln (1+\Delta x/x_0)}{\Delta x/x_0} \]

С помощью логарифмического предельного соотношения при $\Delta x \rightarrow 0$ получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=\frac{1}{x_0} \]

4.1.3 Производная от суммы, произведения и частного функций

Производная возникает в результате предельного перехода. Поэтому свойства пределов приводят к соответствующим свойствам производных.

Теорема. Пусть функции $f(x)$, $g(x)$ дифференцируемы в точке $x$. Тогда
1. Функция $f(x)+g(x)$ также дифференцируема, причем $$(f(x)+g(x))'=f'(x)+g'(x),$$
2. Функция $f(x)\cdot g(x)$ дифференцируема, причем справедлива формула Лейбница $$(f(x)\cdot g(x))'=f'(x)\cdot g(x)+f(x)\cdot g'(x),$$
3. Если $g(x) \neq 0$, тогда $f(x)/g(x)$ дифференцируема в точке $x$, причем $$ \left (\frac{f(x)}{g(x)}\right )'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}.$$

Доказательство.

Важный частный случай. Если $f(x)=const=C$, то $C'=0$ и согласно формуле Лейбница имеем: $$(Cg(x))'=Cg'(x).$$

Примеры.

Задачи.

4.1.4 Производные от сложной функции, от обратной функции, от функции, заданной параметрически

Пусть $y=f(x)$, $z=h(y)$. Подставляя $y$ в аргумент функции $h(y)$, получим композицию функций $z=h(g(x))$ - сложную функцию. Иногда ее обозначают $z=(h\circ g)(x)$. Сложная функция может быть образована композицией и большего числа функций - трех, четырех и т.д.

Пример.

Предположим, что известны производные $dg/dx$, $dh/dy$. Возникает вопрос: как вычислить производную сложной функции $dz/dx$, где $z=h(g(x))$?

Теорема. Пусть $f(x)$ дифференцируема в точке $x=x_0$, $h(y)$ дифференцируема в точке $y_0=f(x_0)$. Тогда $z=h(g(x))$ дифференцируема в точке $x=x_0$, причем \begin{equation} \left. \frac{dz}{dx} \right|_{x=x_0}=\left. \frac{dh}{dy}\right|_{y=f(x_0)}\cdot \left.\frac{df}{dx}\right|_{x=x_0}. (8) \label{comp} \end{equation}

Доказательство.

Замечание. Соотношение (8) содержит в левой части 2 сомножителя - в соответствии с тем, что сложная функция образована композицией двух функций. Если сложная функция образована композицией 3 функций, в левой части имеется 3 сомножителя и т.д.

Напомним, что если задана функция $y=f(x)$, то обратной к ней функцией называется функция $x=h(y)$ со следующими свойствами: $h(f(x))=x$, $f(h(y))=y$. Разумеется, обратная функция существует не всегда.

Теорема. Пусть функция $y=f(x)$ имеет непрерывную производную в некоторой окрестности $V$ точки $x=x_0$, причем $f'(x_0) \neq 0$. Тогда в некоторой окрестности $U \subset V$, $x_0 \in U$, функция $f(x)$ имеет обратную, определенную в некоторой окрестности точки $y_0=f(x_0)$, причем выполняется равенство: \begin{equation} h'(y_0)=\left. \frac{1}{f(x)}\right |_{x=h(y_0)}. (9) \label{inv} \end{equation}

Доказательство.

Примеры.

Далее, пусть для некоторых функций $a(t),b(t)$, заданных на интервале $\left[t_1,t_2\right]$, $x=a(t)$, $y=b(t)$ (в этом случае говорят, что переменные $ x $ и $ y $ заданы параметрически). Предположим, что для функции $x=a(t)$ существует обратная функция $t=\phi (x)$. Тогда $y=b(t)=b(\phi(x))$, так что появляется зависимость между $x$ и $y$. В этом случае говорят, что функция $y(x)$ задана параметрически (с помощью параметра $t$). Если известны производные функций $a(t)$, $b(t)$, то можно вычислить производную функции $y'(x)$.

Теорема. Предположим, что функции $a(t),b(t)$ дифференцируемы на интервале $\left[t_1,t_2\right]$, причем существует обратная функция $t=\phi (x)$, дифференцируемая при всех интересующих нас $x$. Тогда производная $y'(x)$ существует, причем \begin{equation} y'(x)=\left.\frac{b'(t)}{a'(t)}\right |_{t=\phi (x)}. (10) \label{par} \end{equation}

Доказательство.

Задачи.

4.1.5 Таблица производных

Приведем итоговую таблицу производных, включающую производные важнейших функций.

1. $(x^{\alpha})'=\alpha \cdot x^{\alpha -1}.$

2. $(e^x)'=e^x.$

3. $(\sin x)'=\cos x$.

4. $(\cos x)'=-\sin x.$

5. $(\ln x)'=1/x.$

6. $(a^x)'=\ln a\cdot a^x.$

7. $$(tg x)'=\frac{1}{\cos ^2x}.$$

8. $$(ctg x)'=-\frac{1}{\sin ^2 x}.$$

9. $$(\arcsin x)'=\frac{1}{\sqrt{1-x^2}}.$$

10. $$(\arccos x)'=-\frac{1}{\sqrt{1-x^2}}.$$

11. $$(arctg x)'=\frac{1}{1+x^2}.$$

12. $$(arcctg x)'=-\frac{1}{1+x^2}.$$