3. Пределы. Непрерывные функции

3.2.1 Определения

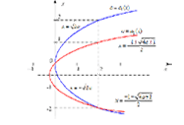
Здесь мы рассматриваем функции, заданные на подинтервале $\left[ a,b\right] \subset \mathbb{R}$. В данном случае можно обсуждать локальное поведение функции в окрестности любой точки $x_0 \in \left[ a,b\right]$, причем к точке можно приближаться разными способами; соответственно, имеется несколько определений предела функции в точке.

Определение. Множество $(x_0-\varepsilon, x_0+\varepsilon)$ при $\varepsilon >0 $ называют окрестностью (или $\varepsilon-$окрестностью) точки $x_0$.

Определение. Конечное число $A$ называется пределом $f(x)$ при $x \rightarrow x_0$, если для любого $\varepsilon >0$ существует такое $\delta >0$, что при всех $x$, удовлетворяющих условию $|x-x_0|<\delta $ выполняется $|f(x)-A|<\varepsilon $.

Обозначение. Этот факт обозначают следующим образом:

\[ \lim _{x\rightarrow x_0}f(x)=A, \]

или

\[ f(x) \xrightarrow[x\to x_0]{} A. \]

Если мы приближаемся к интересующей нас точке слева, конструкцию следует соответствующим образом изменить.

Определение. Конечное число $A$ называется левым пределом $f(x)$ при $x \rightarrow x_0$, если для любого $\varepsilon >0$ существует такое $\delta >0$, что при всех $x$, удовлетворяющих условию $x_0-\delta< x < x_0$ выполняется $|f(x)-A|<\varepsilon $.

Обозначение. Этот факт обозначают следующим образом:

\[ \lim _{x\rightarrow x_0-0}f(x)=A, \]

или

\[ f(x) \xrightarrow[x\to x_0-0]{} A. \]

Аналогичным образом вводится понятие предела справа, обозначается он

\[ \lim _{x\rightarrow x_0+0}f(x)=A, \]

или

\[ f(x) \xrightarrow[x\to x_0+0]{} A. \]

Контрольный вопрос.

Несколько изменяя формулировку бесконечного предела для последовательности, имеем

Определение. Говорят, что функция $f(x)$ имеет в точке $x_0 \in \left[ a,b\right] $ предел $+\infty$, если для любого $A>0$ существует такое $\delta >0$, что при всех $x \in \left[ x_0-\delta, x_0+\delta \right] $ выполняется неравенство $f(x)>A$.

Обозначение. Этот факт обозначают

\[ \lim _{x\rightarrow x_0}f(x)=+\infty, \]

или

\[ f(x) \xrightarrow[x\to x_0]{} +\infty. \]

Далее следует определить левый бесконечный предел, правый бесконечный предел, .....

Контрольный вопрос.

Определение. Если $f(x)$ имеет в точке $x_0$ предел, равный 0, функцию $f(x)$ называют бесконечно малой в точке $x=x_0$. Если $f(x)$ имеет в точке $x_0$ предел, равный $+\infty$, функцию $f(x)$ называют бесконечно большой в точке $x=x_0$.

Теорема. Пусть $f(x)$ имеет в точке $x_0$ предел $A$. Тогда функция $g(x)=f(x)-A$ является бесконечно малой в точке $x=x_0$.

Контрольный вопрос.

3.2.2 Арифметика пределов

Здесь приведена серия теорем, описывающая предел суммы, произведения и частного функций, имеющих в точке $x_0$ конечный предел. Их можно переписать и для случая левых пределов, правых пределов, предельная точка $x_0$ может быть конечной или бесконечной ($x_0=\pm \infty$).

Теорема. Пусть

\[ \lim _{x\rightarrow x_0}f(x)=A, \, \lim _{x\rightarrow x_0}g(x)=B, \]

причем $A$ и $B$ - конечные числа. Тогда функция $(f(x)+g(x))$ имеет в точке $x_0$ конечный предел, причем

\[ \lim _{x\rightarrow x_0}(f(x)+g(x))=A+B. \]

Доказательство.

Теорема. Пусть

\[ \lim _{x\rightarrow x_0}f(x)=A, \, \lim _{x\rightarrow x_0}g(x)=B, \]

причем $A$ и $B$ - конечные числа. Тогда функция $(f(x)\cdot g(x))$ имеет в точке $x_0$ конечный предел, причем

\[ \lim _{x\rightarrow x_0}(f(x)\cdot g(x))=A\cdot B. \]

Теорема. Пусть

\[ \lim _{x\rightarrow x_0}f(x)=A, \, \lim _{x\rightarrow x_0}g(x)=B, \]

причем $A$ и $B$ - конечные числа, $B \neq 0$. Тогда функция $f(x) / g(x) $ имеет в точке $x_0$ конечный предел, причем

\[ \lim _{x\rightarrow x_0}(f(x) / g(x))=A / B. \]

Теорема. Пусть выполняется неравенство $ f(x) < M $ для всех $x$ из некоторой окрестности точки $x_0$, причем существует конечный предел

\[ \lim _{x\rightarrow x_0}f(x) =A . \]

Тогда $A \leq M$ (переход к пределу в неравенствах).

Замечание. Разумеется, существуют аналоги этих теорем и в том случае, когда один из пределов (или оба предела) бесконечен, а также для левых и правых пределов.

3.2.3 Арифметика бесконечно малых

Для функций непрерывного переменного также справедливы теоремы о бесконечно малых. Разумеется, для всех возможных вариантов - когда речь идет о пределе, левом пределе, правом пределе. При этом предельная точка $x_0$ может быть конечной или бесконечной ($x_0=\pm \infty$).

Теорема. Пусть $f(x)$, $g(x)$ - бесконечно малые при $x \rightarrow x_0$. Тогда $(f(x)+g(x))$ - бесконечно малая при $x \rightarrow x_0$.

Теорема. Пусть $f(x)$ - бесконечно малая при $x \rightarrow x_0$, $g(x)$ - ограниченная в окрестности $x=x_0$ функция. Тогда $f(x)\cdot g(x)$ - бесконечно малая при $x \rightarrow x_0$.

Теорема. Пусть $f(x)$ - бесконечно малая при $x \rightarrow x_0$, \[ \lim _{x\rightarrow x_0}g(x)=B, \] причем $B$ - конечное число, $B \neq 0$. Тогда функция $(f(x) /g(x))$ бесконечно малая при $x \rightarrow x_0$.

Определение. Бесконечно малые при $x \rightarrow x_0$ $f(x)$, $g(x)$ называются эквивалентными, если существует предел \[ \lim _{x\rightarrow x_0}f(x)/g(x)=\theta, \] причем $\theta \neq 0$, $\theta \neq \pm \infty$. Этот факт обозначают следующим образом: $f(x) \sim g(x)$ при $x \rightarrow x_0$.

3.2.4 Признаки существования пределов

Следующие теоремы указывают условия, при которых функция имеет предел при $x \rightarrow x_0$.

Теорема. Пусть $f(x)$ - монотонно возрастающая функция, ограниченная сверху. Тогда она имеет конечный предел при $x \rightarrow x_0$.

Следствие. Если $f(x)$ - монотонно возрастающая функция, она имеет пределом либо $+\infty$, либо конечное число.

Соответственно, для монотонно убывающей функции.

Теорема. Пусть $f(x)$ - монотонно убывающая функция, ограниченная снизу. Тогда она имеет конечный предел при $x \rightarrow x_0$.

Теорема. Пусть для всех $x \in (x_0-\varepsilon,x_0+\varepsilon)$ для некоторого $\varepsilon >0$ выполняются неравенства $f(x)\leq g(x) \leq h(x)$, и при $x \rightarrow x_0$ \[ \lim _{x\rightarrow x_0}f(x)=A, \,\lim _{x\rightarrow x_0}h(x)=A. \] Тогда $g(x)$ также имеет предел при $x \rightarrow x_0$, причем \[ \lim _{x\rightarrow x_0}g(x)=A. \]

Критерий Коши. Для того, чтобы функция $f(x)$ имела конечный предел при $x \rightarrow x_0$, необходимо и достаточно, чтобы для любого $ \varepsilon >0$ существовало такое $\delta$, что при всех $x_1,x_2 \in (x_0-\delta, x_0+\delta)$ выполнялось $|f(x_1)-f(x_2)|<\varepsilon $.

3.2.5 Замечательные пределы

Здесь мы приведем основные предельные соотношения, возникающие при т.н. "раскрытии неопределенностей". Представленные ниже соотнрошения "раскрывают неопределенности" вида $ \frac{0}{0} $, $ \frac{\infty}{\infty} $, $ 1^{\infty} $ и т.п. При этом предполагается, что аргумент функции $ x $ стремится к $ 0 $ или $ \infty $. Это не ограничивает общности рассмотрений, потому что конечную точку $x=a$ можно заменой переменной $x=a+x'$ перевести в точку $x'=0$, так что достаточно выписывать соотношения только для точки $x=0$. Далее, по ходу доказательства предельных равенств мы будем использовать тот факт, что все элементарные функции непрерывны в своей области определения. Определение непрерывности мы дадим несколько позже, так что тут мы нарушаем последовательность изложения.

1.Первый замечательный предел.

\[ \lim _{x\rightarrow +\infty}\left (1+\frac{1}{x}\right )^x=e. \]

Доказательство.

3.2.6 Список важнейших предельных соотношений

Имеется список основных предельных соотношений. Он фиксирует поведение основных элементарных функций, когда их аргумент стремится к бесконечности или 0.

1. \[ \lim _{x \rightarrow +\infty } a^x \,= \begin{array}{cc} \infty, &a > 1, \\ 0, & 0 < a< 1 .\end{array} \]

2. \[ \lim _{x \rightarrow -\infty } a^x \,= \begin{array}{cc} 0, & 0 < a <1 \\ \infty , & a >1.\end{array} \]

3. \[ \lim _{x \rightarrow +\infty } \ln x\,= \infty . \]

4. \[ \lim _{x \rightarrow - \infty } \ln x\,= 0 . \]

5. \[ \lim _{x \rightarrow +\infty } x^b \,= \begin{array}{cc} \infty, & b > 0, \\ 0, & 0< b <1 .\end{array} \]

6. \[ \lim _{x \rightarrow +0 } x^b \,= \begin{array}{cc} 0, & b > 0, \\ +\infty , & 0< b < 1 .\end{array} \]

7. \[ \lim _{x \rightarrow +\infty }x^{\frac{1}{x}}=1. \]

8. Если $a>1$, то при любом $b$ \[ \lim _{x \rightarrow +\infty } \frac{a^x}{ x^b} \,= +\infty. \]

9. Если $b>0$, то \[ \lim _{x \rightarrow +\infty } \frac{ x^b}{ \ln x} \,= +\infty. \]

Два последних предельных отношения "сравнивают" между собой бесконечно большие при $x \rightarrow +\infty$ функции $a^x, \, x^b, \, \ln x$.

Примеры вычисления пределов.

Задачи.